Org-mode e Python

Por si só, a linguagem informática python, não tem grande significado para mim. É certo que se consegue fazer excelentes análises através desta ferramenta, mas falando na qualidade de um não programador, não tenho os conhecimentos nem o tempo, para elaborar longas listas de código (informático) para poder executar um processo complexo de análise. No entanto, se junto com python, usarmos um editor de texto como o emacs, mais propriamente o sistema org-mode do emacs, ficamos na posse de uma ferramenta que em muito supera qualquer um dos produtos da Microsoft. Todo este website é escrito em org-mode do emacs sendo depois passado para a internet e guardado no GitHub.

A primeira equação que se aprende na prática de betão armado:

\[{ \mu }=\frac { { M }_{ rd } }{ b\times { d }^{ 2 }\times { f }_{ cd } }\]

Um exemplo simples da utilização de python, é no cálculo armadura necessária em uma viga à flexão. Os cálculos em sí não tem nada de complicado e qualquer máquina de calcular os faz. Mas obter os resultados em forma de tabela, prontos a serem incluídos em documentação da obra ou a serem compartilhados aqui neste website, é uma grande mais valia.

Os valores das variáveis foram introduzidos em uma outra secção do documento, e por isso não são apresentados no código em python. No entanto, elas são apresentadas no resultado final. De qualquer maneira é apresentado no bloco que se segue, os seus valores:

Variáveis:
+ Mrd=61.2
+ h=0.5 
+ fcd=13.33 
+ b=.3
+ fsyd=348
+ fctm=2.2
+ fyk=400

O bloco aonde são introduzidas as fórmulas necessárias para o desenvolvimento do cálculo:

import pandas as pd
from sympy import *
d=0.9*h
Ac=h*b
u=float(Mrd/(fcd*1000*d**2*b))
W=1-sqrt(1-2*u)
As= (W*b*d*(fcd/fsyd)*10**4).n(2)
Asmax=(0.04*Ac*10**4)
Asmin= (0.26*(fctm/fyk)*b*d*10**4)
Asmin_Verif=0.0013*b*d*10**4
def verifica(Asmin):
    if Asmin >= 0.0013*b*d*100:
        verifica = print ("Verifica Condicoes pelo EC")
    else:
        verifica = print("NAO VERIFICA")
    return verifica
Descricao=["Momento Resistente (kN/m)","Altura Total h (m)", "d (m)", 
           "fcd (mPa)", "b (m)","Momento Reduzido ", 
           "W", "fsyd (mPa)", "Area armadura (cm2)", "Area de Betao, m2", 
           "Area Maxima armadura,cm2", "fctm, mPa", "fyk, mPa",
           "Area minima armadura, cm2", "Verificacao Area minima, cm2"]
Resultados=[Mrd, h, d, fcd, b, u, W, fsyd, As, Ac, 
            Asmax,fctm, fyk, Asmin, Asmin_Verif ]
data = {'Descricao' : pd.Series(Descricao), 
        'Resultados' : pd.Series(Resultados)}
tabela = pd.DataFrame(data)
print(tabela)
print("Verificacao:  As,min = ",Asmin, " cm2 > 0,0013xbtxd = ", Asmin_Verif, "cm2" )
verifica(Asmin)

E por fim obtemos uma tabela com os vários resultados. A partir do momento que o bloco da introdução de dados está feito, pode ser reaplicado em outras vigas que estejam sujeitas (neste caso somente) à flexão.

                       Descricao          Resultados
0      Momento Resistente (kN/m)                61.2
1             Altura Total h (m)                 0.5
2                          d (m)                0.45
3                      fcd (mPa)               13.33
4                          b (m)                 0.3
5              Momento Reduzido            0.0755744
6                              W  0.0786688425629442
7                     fsyd (mPa)                 348
8            Area armadura (cm2)                 4.1
9              Area de Betao, m2                0.15
10      Area Maxima armadura,cm2                  60
11                     fctm, mPa                 2.2
12                      fyk, mPa                 400
13     Area minima armadura, cm2              1.9305
14  Verificacao Area minima, cm2               1.755
Verificacao:  As,min =  1.9305000000000003  cm2 > 0,0013xbtxd =  1.7550000000000001 cm2
Verifica Condicoes pelo EC

Os cálculos foram feitos de acordo com as normas do Eurocódigo.

Um outro exemplo de como se pode usar python e desta vez recorrendo a duas das muitas packages (Matplotlib e Numpy) disponíveis para esta linguagem, pode-se obter resultados gráficos para um dado problema. Neste exemplo, é dito ao editor para processar uma imagem de um gráfico de uma função \(f(x)=x^{2}\).

Assim, começamos por introduzir os dados em um bloco e a ditar os nossos termos para a configuração do gráfico:

import matplotlib.pyplot as plt
import numpy as np
fig=plt.figure(figsize=(6,4))
x=np.linspace(-1,1)
plt.plot(x**2 )
plt.grid(True)
plt.xlabel('Distância')
plt.ylabel("Altura")
plt.title('Titulo',fontsize=14)
plt.text(20, 0.6, 'Indicador')
plt.savefig("images/elevado.png")
return "images/elevado.png"

E o resultado, ou seja, a função \(f(x)=x^{2}\) é apresentada de seguida:

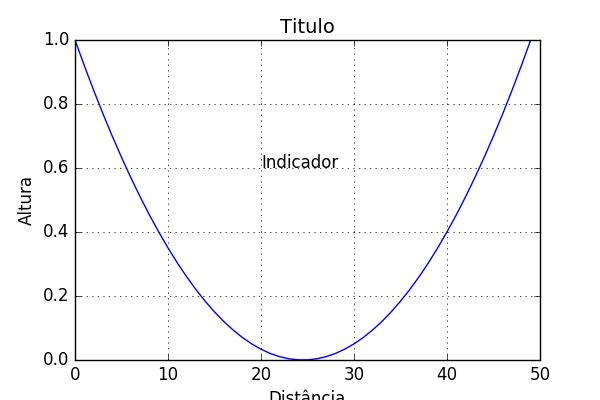
Com esta breve introdução, fica apresentado o modo de como é feito a análise em org-mode e python (sendo o mesmo aplicado para outras linguagens informáticas).

O bloco referente à introdução de dados, e em referência ao desenvolvimento deste website, só será mostrado caso faça sentido na exposição de uma ideia ¹. É minha intenção, dedicar este espaço, ao desenvolvimento e análise de situações da/e na construção civil, deixando para os especialistas em informática, o desenvolvimento da programação.