Derivação, Integração e incógnita de uma equação,

O texto desta página, em formato PDF.

Matemática e Python na vertente da Engenharia Civil

Através da utilização de Python como uma calculadora, é possível a obtenção dos resultados, para três categorias de cálculos matemáticos, bastante comuns em Engenharia Civil. Essas três (categorias) de cálculo são, a integração, a derivação, e a descoberta de uma incógnita numa equação.

O uso de Python, não é um substituto para softwares como o Robot da Autodesk, ou para uma máquina de calcular moderna. No entanto, apresenta vantagens em relação a estes, especialmente quando se pretende compartilhar os resultados ou ter várias pessoas a trabalhar no mesmo projeto. Um exemplo disso, é o PDF produzido com este artigo, escrito na sua totalidade em Jupyter (usando Python). Utilizando sempre o mesmo software, foi produzido o documento final, que contém a informação dos cálculos, gráficos e a informação textual, estando já pronto a ser apresentado ao cliente ou a ser compartilhado com os outros membros da equipa.

SymPy é uma biblioteca Python para matemática simbólica. Ele pretende-se tornar um sistema completo de álgebra para computador (computer algebra system-CAS) mantendo o código o mais simples possível, de modo a ser compreensível e facilmente extensível. SymPy é escrito inteiramente em Python.

-– traduzido da página SymPy na internet

No entanto, e para cálculo matemático avançado, NumPy, também uma livraria para Python, torna-se a melhor opção.

Embora a Numpy também realize os cálculos deste artigo, e tendo em conta a simplicidade dos mesmos cálculos, não faz sentido a usar, especialmente porque requer mais linhas de código, para fazer a mesma computação.

NumPy é uma biblioteca fundamental para a computação científica em Python. É uma biblioteca Python que fornece um objeto de matriz multidimensional, vários objetos derivados (como matrizes mascaradas e matrizes), e uma variedade de rotinas para operações rápidas em matrizes, incluindo matemática, lógica, manipulação de forma, classificação, seleção, I/O, transformações originais de Fourier, álgebra linear básica, operações estatísticas básicas, simulação aleatória e muito mais.

-– traduzido da página NumPy documentation — NumPy v1.22 Manual

Ao longo deste artigo, será apresentado de uma forma simples, recorrendo ao cálculo dos esforços numa viga, como com Python, consegue-se obter os resultados para a integração, derivação e a descoberta do valor de uma incógnita, numa equação.

Iniciamos então, com a ativação da livraria de Sympy, como apresentado no sript seguinte.

from sympy import* 
x, y, z = symbols("x, y, z", real=True)` 
init_printing(use_latex="mathjax")

Reparar que o uso de init_printing(use_latex="mathjax"), só faz sentido quando se utiliza o Jupyter Notebook, pois vai permitir, que os resultados sejam apresentados já formatados e convertidos de LaTeX.

Exemplo - Viga Simples

Condições Iniciais

Viga com 10 metros de comprimento, assente em dois apoios simples.

Carga de $1 kN\m$, aplicada ao longo de todo o comprimento da viga.

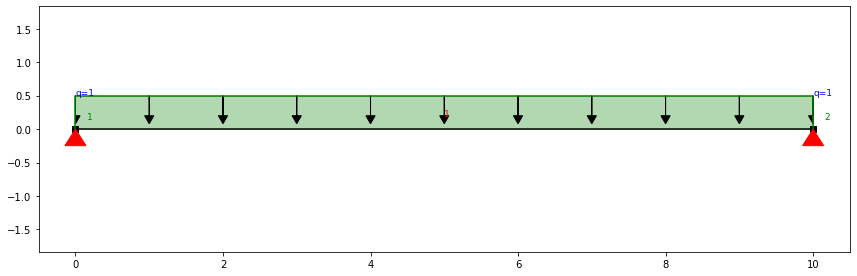
As reações nos apoios ( $R{1}$, $R{2}$ ) , são de $5kN$ em ambos.

O cálculo das reações nos apoios, também poderia ser feito com um dos módulos de Sympy. No link em baixo, existem vários exemplos de como este módulo pode ser usado no cálculo dos esforços e em situações muito mais complexas, que a do exemplo deste artigo.

Solving Beam Bending Problems using Singularity Functions — SymPy 1.9 documentation

Para encontar as reações nos apoios ($R{1}, R{2}$) da viga do exemplo, bastam as seguintes linhas de código

from sympy.physics.continuum_mechanics.beam import Beam
E, I = symbols('E, I')
R1, R2 = symbols('R1, R2')
b = Beam(10, E, I)
b.apply_load(-1, 0, 0)
b.apply_load(R1, 0,-1) 
b.apply_load(R2, 10,-1)
b.solve_for_reaction_loads(R1, R2)
b.reaction_loads

Sendo o resultado e tal como seria de esperar:

$\left { R{1} : 5, \ R{2} : 5 \right }$

Incógnita numa equação

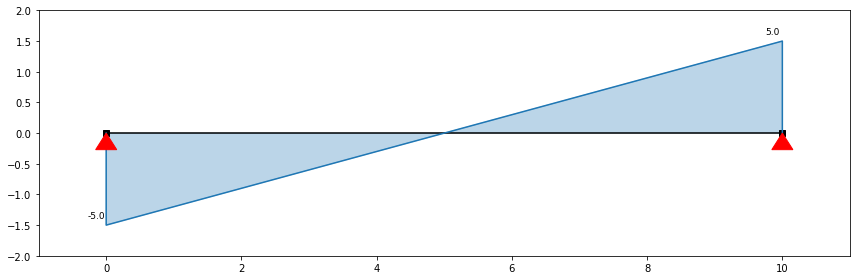
A linha da reta do esforço transverso ($V$), entre o ponto de 0 m e o de 10 m, tem a seguinte função:

$$V_{(x)}~=~5-q \times x$$

Mas como o valor da carga distribuída ($q$) é igual a $1 kN/m$, é possível fazer a simplificação da equação do Esforço Transverso:

$$V{(x)}~=~5-q \times x~ \Longleftrightarrow V{(x)}~= 5-x$$

Devido à simplicidade do exemplo, é imediata a conclusão, que o Momento Máximo, ocorre a meio vão, ou seja, aos 5 metros.

Recorrendo a Sympy e ao comando solve, é possível localizar, para que valor do comprimento, o Momento Fletor é máximo. O Momento Máximo ocorre quando o Esforço Transverso é zero, portanto, igualando a equação da reta, $V_{(x)}=0$, é obtida a localização do Momento Máximo.

V=5-x   # Equação do Esforço Transverso
solve(Eq(V,0),x)  

$\displaystyle \left[ 5\right]$

E como esperado, o resultado é 5 (metros).

Exemplos do comando solve

Exemplo 1 $$ x^{2}=25 \Rightarrow x=-5,x=5 $$

solve(Eq(x**2,25),x)

$\displaystyle \left[ -5, \ 5\right]$

Exemplo 2
Uso do comando solve, em um sistema com duas incógnitas

$$x+5y=2~, -3x+6y=15 ~ \Rightarrow ~x=-3~, ~y=1$$ :

solve([Eq(x + 5*y, 2), Eq(-3*x + 6*y, 15)], [x, y])

$\displaystyle \left{ x : -3, \ y : 1\right}$

Ou então, e escrevendo a equação de outro modo (ao não usar Eq, Sympy assume que a expressão matemática é igual a zero):

solve([x + 5*y - 2, -3*x + 6*y - 15], [x, y])

$\displaystyle \left{ x : -3, \ y : 1\right}$

Integração

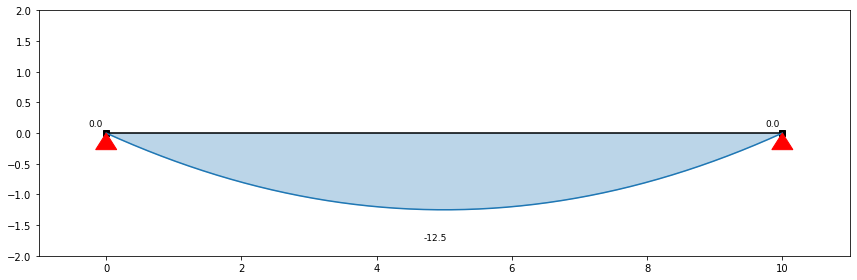
A equação da curva do Momento Fletor, não é mais que a soma da área, compreendida entre a reta do Esforço Transverso e o eixo do x. Por outras palavras, a Integral da reta do Esforço Transverso, é o mesmo, que a expressão matemática da curva do Momento Fletor.

$${M}_{(x)}=\int \left(5 - x\right)\, dx= - \frac{x^{2}}{2} + 5 x+C$$

Comando integrate

Em Sympy, o comando integrate, é usado na resolução da integração. Estando a equação da reta previamente definida, $V_{(x)}=5-x$, basta escrever o comando integrate(V), para ser efetuada a operação.

integrate(V)

$\displaystyle - \frac{x^{2}}{2} + 5 x$

E para escrever a integral, é usado o comando Integral.

Para escrever a Integral da função $V_{(x)}$:

Integral(V,x)

$\displaystyle \int \left(5 - x\right)\, dx$

Sabendo que o Momento Máximo ocorre em $x=5$, podemos substituir o $x$ da integral, por 5. Para tal, usamos o comando subs(), e passamos a informação do que queremos substituir. Neste caso, o $x$ por 5.

integrate(V).subs(x,5)

$\displaystyle \frac{25}{2}$

O valor do Momento Máximo é de $\frac{25}{2}=12.5~kN/m$.

Embora esta seja uma fração simples, em que seja possível realizar o cálculo mental imediato da mesma, o mesmo pode não ser verdade com outros resultados. Para obter o resultado na forma decimal, o comando n()deve ser adicionado.

integrate(V).subs(x,5).n()

$\displaystyle 12.5$

Confirmando o resultado obtido, com a fórmula do Momento Máximo para uma viga como a do exemplo:

$$M_{max}=\frac{qL^{2}}{8}=\frac{1 \times 10^{2}}{8}=12.5~kN/m $$

Derivação

Por vezes queremos trabalhar no sentido inverso, e descobrir o valor do Esforço Transverso, a partir da equação do Momento Fletor.

$${V}_{(x)}=\frac{d}{d x} \left(- \frac{x^{2}}{2} + 5 x\right)= 5 - x$$

Comando diff

Com o comando diff de Sympy, é realizada a derivação de uma expressão matemática.

Como determinado, a equação da curva do Momento Fletor, é o resultado da integração da reta do Esforço Transverso:

$$M_{(x)}= - \frac{x^2}{2}+5x = \int (5-x) \text{dx} $$

Escrevendo diff(integrate(V,x)), dizemos a Sympy, para derivar o resultado da integração da reta do Esforço Transverso.

diff(integrate(V,x))

$\displaystyle 5 - x$

Também designar uma qualquer letra(s) para a Integração, e depois usar no comando diff essa(s) mesma(s) letra(s).

MV=integrate(V,x)  # atribuição da designação "MV" à integração

diff(MV)   # Derivar a expressão, usando a nova designação

$\displaystyle 5 - x$