Viga/Laje com 3 apoios simples e dois vãos
Python Script: f_3apoios.py
Luis Moura / 2019-07-12
O texto desta página, encontra-se em formato PDF, e pode ser acedido aqui.
Introdução
Um dos casos mais comuns na análise de uma viga ou laje, é quando existe dois vãos e um carregamento uniforme em cada um dos vãos. A análise permite determinar os momentos positivos e negativos máximos, necessários para o cálculo da armadura.
Para fazer essa análise, eu criei um pequeno Python script,1 em que com o apoio da python package anaStruct,2 possa ser facilmente determinado os valores pretendidos.
A invocação do script é feita através de:
f_3apoios(L_span1,L_span2,q1,q2,load_factor), em que:
- L_span1 = Distância entre apoios do primeiro vão (m)
- L_span2 = Distância entre apoios do segundo vão (m)
- q1 = Carga do primeiro vão
- q2 = Carga do segundo vão
- load_factor = Factor de segurança aplicado ao carregamento
Estrutura
Um dos casos mais comuns em engenharia civil, é o da viga/laje apoiada em três apoios simples e com dois vãos - Figura 1.

Figure 1: Estrutura com dois vãos de igual dimensão (4 metros) e com carregamento uniforme ao longo de ambos os vãos
No entanto, nem sempre os vãos têm a mesma dimensão, nem as cargas são uniformes a ambos os vãos. Nesse caso, basta modificar o dimensionamento e carregamento na altura de executar o script. Por exemplo, uma laje com um vão de 4 metros e carregamento de 8kN e um segundo vão de 5 metros e um carregamento de 9kN, é executado da seguinte maneira (Figura 2):
f_3apoios(4,5,8,9,1)
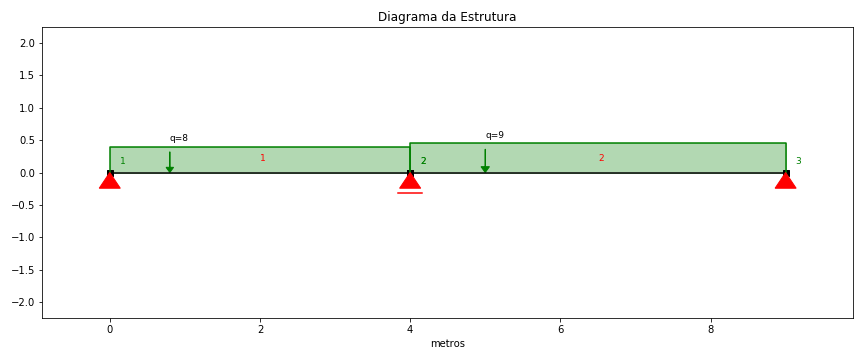
Figure 2: Laje com vão de 4 metros e carregamento de 8kN, e vão de 5 metros e carregamento de 9kN. O fator de segurança utilizado é 1 (F.S. nulo)
Diagrama Momento Fletor
Para além do diagrama da estrutura, o scrip também produz o diagrama do momento fletor, de especial interesse para a determinação da armadura a utilizar na construção da viga ou laje.3
Criando por exemplo uma estrutura com dois vãos, em que o primeiro tem 4 metros e o segundo com 5 metros, com carregamento de 5kN e 6.4kN respectivamente, podemos dar início à análise:
f_3apoios(4,5,5,6.4,1.35)
Neste caso, será utilizado um F.S=1.35.
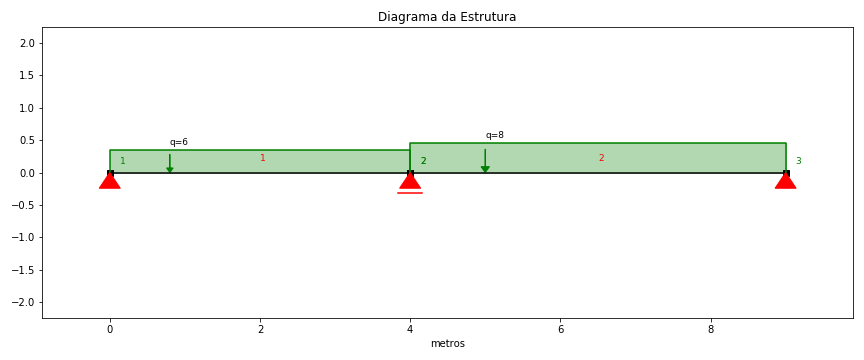
Figure 3: Laje com vão de 4 e 5 metros, e carregamento de 5kN e 6.4kN respectivamente. Ao carregamento, foi aplicado um fator de segurança de 1.35
Criada a estrutura, o script produz o diagrama de momento fletor para a mesma.
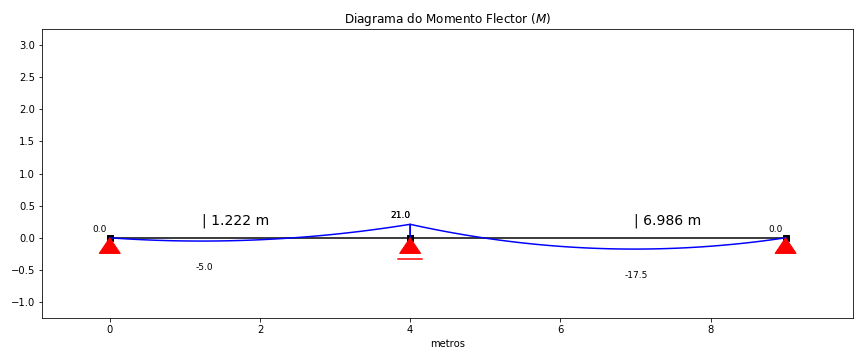
Figure 4: Diagrama do momento fletor para a laje. Reparar que os momentos positivos em ambos os vãos são apresentados com o sinal (-) e o momento negativo sobre o apoio central é apresentado com o sinal (+). Isto deve-se ao facto de ‘anaStruct’ não seguir a convenção do Eurocódigo. Resolvi, por enquanto, não alterar o código e deixa-lo como foi concebido originalmente, no entanto, o texto final do ‘script’, é apresentado de acordo com a convenção do Eurocódigo
No final do script é produzido um texto com as seguintes indicações:
- Localização do Momento Máximo Positivo no primeiro vão e seu respectivo valor.
- Localização do Momento Máximo Positivo no segundo vão e seu respectivo valor.
- Valor do Momento Máximo negativo
A localização do Momento Máximo positivo no primeiro vão ocorre aos 1.22 metros e é de 5.04 kNm
A localização do Momento Máximo positivo no segundo vão ocorre aos 6.99 metros e é de 17.518 kNm
O Momento máximo negativo é de 21.0 kNmA localização do momento máximo negativo não é indicada em texto. Nas estruturas de dois vãos de dimensões semelhantes e carregamentos iguais ou aproximados, o momento máximo negativo acontece sempre no apoio central.
Conclusão
Existem alguns condicionalismo na análise feita pelo script, mas normalmente elas acontecem quando é feita análise pouco prováveis, como por exemplo, um vão com carregamento nulo ou então, vãos com espaçamento entre apoios bastante diferentes. Nestas situações, existe uma grande probabilidade de os resultados serem irrealistas.
O script também necessita de ter os resultados verificados em mais situações correntes, de modo a poder ser utilizado posteriormente em situações de análise real.
No entanto, o objectivo principal do script é cumprido. Através dos resultados obtidos, pode-se depois fazer o dimensionamento da armadura de distribuição. Ao script também pode ser adicionado código, que proponha vários tipos de armadura de acordo com os resultados. No entanto, para o fazer e se for seguido o processo do EuroCódigo, é necessário ter em conta várias variáveis, que dificultam a produção de um scriptque acima de tudo, pretende-se que seja de fácil utilização.
O mesmo processo de cálculo pode ser também feito em software especializado para o efeito, como por exemplo Robot,4 mas é meu objectivo, que a análise e a produção de documentação final a ser entregue às outras equipas do projeto de construção civíl, seja realizado pelo mesmo software, como é o caso deste documento em PDF. Tanto os cálculos executados pelo script, como o texto e produção do PDF, foram realizados em Jupyter Notebook. Deste modo e de uma forma simples, tanto cálculo como o texto são realizados e executados pelo mesmo sistema,5 evitando assim erros, facilidade em correcções ou alterações e rapidez na criação de documentação.
f_3apoios.py
Python script para análise estrutural:
from anastruct.fem.system import SystemElements
import matplotlib.pyplot as plt
from sympy import*
init_printing(use_latex="mathjax")
x,y=var("x y",real=True)
from sympy.utilities.lambdify import lambdify
import numpy as np
def f_3apoios(L_span1,L_span2,q1,q2,load_factor):
"""
Localizar na viga o ponto de Momento Máximo Positivo e negativo.
Viga com 3 apoios e carga igualmente distribuída.
M_max acontece quando V(y)=0
L_span1 = Distância entre apoios do primeiro vão (m)
L_span2 = Distância entre apoios do segundo vão (m)
q1 = Carga do primeiro vão
q2 = Carga do segundo vão
load_factor = Factor de segurança aplicado ao carregamento
EA = Young's modulus * Area
EI = Young's modulus * moment of Inertia
"""
L=L_span1+L_span2
q_span1=load_factor*q1
q_span2=load_factor*q2
q=q_span1+q_span2
EA=15000
EI=5000
# Estrutura
ss = SystemElements(load_factor=1,EA=EA, EI=EI)
ss.add_element(location=[[0, 0], [L_span1, 0]]) #Vão 1
ss.add_element(location=[[L_span1,0],[L,0]]) #Vão 2
ss.add_support_hinged(node_id=1) #Suporte 1
ss.add_support_roll(node_id=2, direction=2) #Suporte 2
ss.add_support_hinged(node_id=3) #Suporte 3
ss.q_load(element_id=[1], q=-q_span1, direction='element') #Carga Vão 1
ss.q_load(element_id=[2], q=-q_span2, direction='element') #Carga Vão 2
ss.solve()
fig=ss.show_structure(show=False,
figsize=(12,5),
scale=0.6)
plt.title("Diagrama da Estrutura")
plt.xlabel("metros")
plt.tight_layout()
plt.show()
# Apoios Força Vertical, Fy:
Fy_1=round(ss.get_node_results_system(node_id=1)["Fy"],3)
Fy_2=round(ss.get_node_results_system(node_id=2)["Fy"],3)
Fy_3=round(ss.get_node_results_system(node_id=3)["Fy"],3)
x=var("x",interval=(0, L))
def func_Fy(x):
if (x == 0):
return Fy_1+ q_span1 * x
elif (x > 0) & (x < L_span1):
return Fy_1+ q_span1 * x
elif (x==L_span1):
return Fy_1+ q_span1*L_span1+ Fy_2
elif (x>L_span1) & (x<L):
return Fy_1+ q_span1*L_span1+Fy_2+q_span2*(x-L_span1)
else:
return 0
# Dimensão vão 1 para Mmax(+)
zero=np.max(solve(Eq(func_Fy(x),0),x))
# momento máximo negativo:
M_negativo=round(integrate(func_Fy(x),(x,0,L_span1)),2)
# Dimensão vão 2 para Mmax(+)
zero_1=L_span1+np.max(solve(Eq(func_Fy(L_span1)+q_span2*x),x))
# Momento Máximo (+) para vão 2
M_positivo_2=round(ss.get_element_results(element_id=2)["Mmin"],3)
# Gráfico Momentos
fig=ss.show_bending_moment(show=False,
offset=(0,-1),
figsize=(12,5),
scale=0.6,
factor=.01)
plt.title("Diagrama do Momento Flector ($M$)")
plt.xlabel("metros")
plt.tight_layout()
plt.text(zero,0.2,f"| {round(zero,3)} m", fontsize=14)
plt.text(zero_1,0.2, f"| {round(zero_1,3)} m",fontsize=14)
plt.show()
print(f"A localização do Momento Máximo positivo no primeiro vão\
ocorre aos {zero:.3} metros\
e é de {integrate(func_Fy(x),(x,0,zero)):.3} kNm")
print(f"A localização do Momento Máximo positivo no segundo vão\
ocorre aos {zero_1:.3} metros\
e é de {-M_positivo_2} kNm")
print(f"O Momento máximo negativo é de {M_negativo} kNm") Welcome to anaStruct’s documentation! — anaStruct 1.0 documentation↩
Este script foi criado para ser executado essencialmente no cálculo das armaduras de uma laje, ignorando o esforço transverso. Para uma viga, é essencial o cálculo do esforço transverso. Em uma laje comum, em que os carregamentos e vãos estejam dentro da normalidade, o esforço transverso não é determinante no cálculo da armadura de distribuição.↩
Robot Structural Analysis Professional | Structural Analysis Software | Autodesk↩
Para sistemas estruturais de maior complexidade, o uso de software especializado é inevitável.↩
