Reforço de uma viga de betão armado para um edifício existente
Reabilitação
Luis Moura / 2019-04-14
Avaliação da capacidade resistente e dimensionamento de uma solução de reforço de uma viga de betão armado para um edifício existente. Existe a necessidade de aumentar a resistência da viga à flexão e ao corte em 30%, devido a alterações das condições de uso do piso suportado pela viga.
O texto desta página, encontra-se em formato PDF, e pode ser acedido aqui.
Introdução
Em análise, estão um conjunto de 3 vigas existentes em um prédio. Todas as 3 vigas apresentam caracteristicas distintas, com vãos e áreas e posicionamento de armadura distintas, sendo portanto necessário fazer a sua análise individualmente. Para a viga localizada no maior vão, será denominada ao longo deste relatório de Viga #1. A viga existente no vão de menor comprimento, será denominada de Viga #2 e a restante viga que é uma consola, de Viga #3. De notar que embora com características diferentes, todas as 3 vigas encontram-se alinhadas sobre o mesmo eixo.
O aço a usar no reinforço é um S500 e a classe de betão é C25/30.
| Classe | \(f_{cK} (mPa)\) | \(\gamma_{c}\) | \(f_{cd} (mPa)\) |
|---|---|---|---|
| C25/30 | 25 | 1.5 | 16.666667 |
Para o aço e para o betão, foi considerado um coeficiente de segurança, \(\gamma_{c}\) e \(\gamma_{s}\) de 1,5 e 1,15 respectivamente, que é o valor recomendado pelo Eurocódigo.
| Classe | \(f_{yK} (mPa)\) | \(\gamma_{c}\) | \(f_{yd} (mPa)\) |
|---|---|---|---|
| S500 | 500 | 1.15 | 434.78261 |
Não foi dada nenhuma informação inicial sobre os esforços existentes e atuantes sobre as 3 vigas em consideração neste trabalho. É pois considerado que as condições existentes igualam ou superam, os requisitos minímos de segurança para estruturas de betão armado, como definido pelo Eurocódigo.
Análise da Capacidade Resistente à Flexão e ao Corte
Viga #1
As caracteristicas da viga 1 são apresentadas em tabela e na imagem 1. O comprimento de vão efectivo entre apoios para esta viga é de 7 metros, sendo a distância livre entre faces dos apoios, \(l_{n}\) ligeiramente inferior a esse valor.
| b (m) | h (m) | Armadura Inferior | \(A_{s,inf} (cm^{2})\) | Armadura Superior | \(A_{s,sup}( cm^{2})\) | Estribos |
|---|---|---|---|---|---|---|
| 0.3 | 0.5 | \(3\phi 20+2\phi25\) | 19.24 | \(4\phi 16\) | 8.04 | \(\phi 6//0.2\) |
| \(3\phi 20\) | \(2\phi25\) | \(4\phi 16\) | \(\phi 6//0.2\) | 2 ramos \(\phi 6//0.2\) |
|---|---|---|---|---|
| 9.42 | 9.82 | 8.04 | 1.41 | 2.82 |
Visto não ser uma viga em “T”, não se teve em consideração a possível contribuição da laje para a largura efectiva do banzo, \(b_{eff}\), como descrito na secção 5.3.2.1 do EC2.
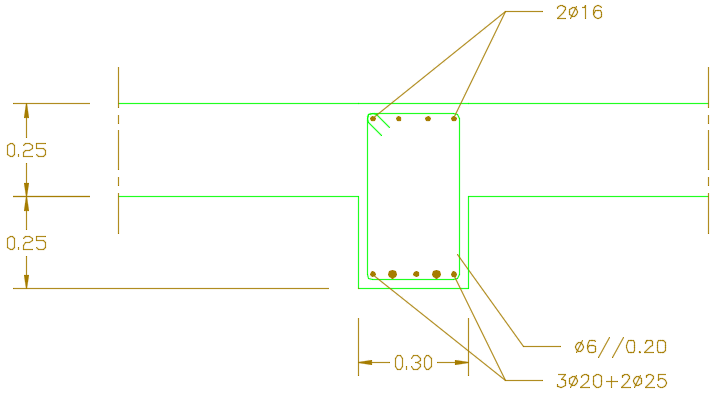
Figure 1: Viga 1
Determinação do Momento Resistente da Viga #1
O momento resistente é determinado através da seguinte equação:
\[\begin{equation} M_{rd}=A_{s} \times f_{yd} \times Z \end{equation}\]em que:
- \(M_{rd}\) é o valor de cálculo do momento flector resistente
- \(A_{s}\) é a área de aço à tração da secção
- \(f_{yd}\) é valor de cálculo da tensão de cedência do aço
- Z é o braço do binário de forças interiores em flexão
De uma forma simplificada, podemos considerar que \(Z=0,81 \times h\), em que “h” é a altura da secção da viga.
Somente a área de armadura à tração, ou seja, a armadura inferior, é considerada no cálculo do Momento Resistente. São desprezadas as contribuições do aço à compressão e do betão, à tração.
| \(A_{s} (cm^{2})\) | \(f_{yd} (mPa)\) | h (m) | Z (m) | \(M_{rd} (kN.m)\) |
|---|---|---|---|---|
| 19.24 | 434.78 | 0.5 | 0.405 | 338.79 |
O valor do Momento Resistente para a viga 1 é de 338.7892716 kN.m.
Determinação do Esforço Transverso da Viga 1
O cálculo do Esforço Transverso máximo permitido para o Estado Limite Último da viga #1, tendo em conta as condições estruturais implementadas, é feito de acordo com a seguinte equação:
\[\begin{equation} V_{rd}=(\frac{A_{sw}}{S}) \times Z \times f_{yd} \times cot\phi \end{equation}\]em que:
- \(V_{rd}\) é o valor de cálculo do esforço transverso
- \(A_{sw}\) é a área de armadura da secção
- \(S\) é o espaçamento entre armadura
- \(f_{yd}\) é valor de cálculo da tensão de cedência do aço
- Z é o braço do binário de forças interiores em flexão
Tal como na análise da resistência à flexão da Viga #1, também aqui, o valor de Z pode ser calculado por \(Z=0,81 \times h\), em que “h” é a altura da secção da viga.
| \(A_{sw} (cm^{2})\) | S (m) | h (m) | Z (m) | \(f_{yd} (mPa)\) | \(\phi\) | \(V_{rd} (kN)\) |
|---|---|---|---|---|---|---|
| 2.82 | 0.2 | 0.5 | 0.405 | 434.78 | 1 | 248.28 |
Tendo sido analisadas as presentes condições estruturais, e respeitando os níveis de segurança recomendados pelo EC2, o máximo valor de esforço transverso na viga #1, \(V_{rd}\), é de 248.281119 kN.
Viga #2
As caracteristicas da viga 2 são apresentadas em tabela e na imagem 2. O comprimento de vão efectivo entre apoios para esta viga é de 4 metros, sendo a distância livre entre faces dos apoios, \(l_{n}\) ligeiramente inferior a esse valor.
| b (m) | h (m) | Armadura Inferior | \(A_{s,inf} (cm^{2})\) | Armadura Superior | \(A_{s,sup}( cm^{2})\) | Estribos |
|---|---|---|---|---|---|---|
| 0.45 | 0.25 | \(4\phi 12+2\phi16\) | 8.54 | \(2\phi 16 + 4 \phi 20\) | 16.59 | \(\phi 6//0.2\) |
| (4 ramos) |
| \(4\phi 12\) | \(2\phi16\) | \(4 \phi 20\) | 4 ramos \(\phi 6//0.2\) |
|---|---|---|---|
| 4.52 | 4.02 | 12.57 | 5.64 |
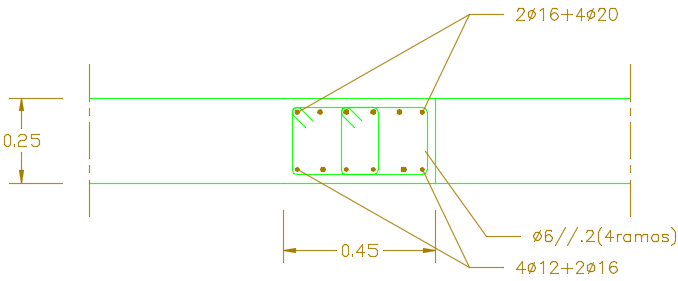
Figure 2: Viga 2
Determinação do Momento Resistente da Viga #2
O momento resistente é determinado através da seguinte equação:
\[\begin{equation} M_{rd}=A_{s} \times f_{yd} \times Z \end{equation}\]em que:
- \(M_{rd}\) é o valor de cálculo do momento flector resistente
- \(A_{s}\) é a área de aço à tração da secção
- \(f_{yd}\) é valor de cálculo da tensão de cedência do aço
- Z é o braço do binário de forças interiores em flexão
De uma forma simplificada, podemos considerar que \(Z=0,81 \times h\), em que “h” é a altura da secção da viga.
Somente a área de armadura à tração, ou seja, a armadura inferior, é considerada no cálculo do Momento Resistente. São desprezadas as contribuições do aço à compressão e do betão, à tração.
| \(A_{s} (cm^{2})\) | \(f_{yd} (mPa)\) | h (m) | Z (m) | \(M_{rd} (kN.m)\) |
|---|---|---|---|---|
| 8.54 | 434.78 | 0.25 | 0.2025 | 75.19 |
O valor do Momento Resistente para a viga 1 é de 75.19 kN.m.
Determinação do Esforço Transverso da Viga 2
O cálculo do Esforço Transverso máximo permitido para o Estado Limite Último da viga #1, tendo em conta as condições estruturais implementadas, é feito de acordo com a seguinte equação :
\[\begin{equation} V_{rd}=(\frac{A_{sw}}{S}) \times Z \times f_{yd} \times cot\phi \end{equation}\]em que:
- \(V_{rd}\) é o valor de cálculo do esforço transverso
- \(A_{sw}\) é a área de armadura da secção
- \(S\) é o espaçamento entre armadura
- \(f_{yd}\) é valor de cálculo da tensão de cedência do aço
- Z é o braço do binário de forças interiores em flexão
Tal como na análise da resistência à flexão da Viga #1, também aqui, o valor de Z pode ser calculado por \(Z=0,81 \times h\), em que “h” é a altura da secção da viga.
| \(A_{sw} (cm^{2})\) | S (m) | h (m) | Z (m) | \(f_{yd} (mPa)\) | \(\phi\) | \(V_{rd} (kN)\) |
|---|---|---|---|---|---|---|
| 5.64 | 0.2 | 0.25 | 0.2025 | 434.78 | 1 | 248.28 |
Tendo sido analisadas as presentes condições estruturais, e respeitando os níveis de segurança recomendados pelo EC2, o máximo valor de esforço transverso na viga #2, \(V_{rd}\), é de 248.28 kN.
Viga #3
As caracteristicas da viga 3 são apresentadas em tabela e na imagem 3. Sendo esta viga uma consola, tem um comprimento total de 2 metros desde o apoio até ao extremo oposto.
| b (m) | h (m) | Armadura Inferior | \(A_{s,inf} (cm^{2})\) | Armadura Superior | \(A_{s,sup}( cm^{2})\) | Estribos |
|---|---|---|---|---|---|---|
| 0.45 | 0.25 | $4φ 12 $ | 4.52 | \(2\phi 16 + 2 \phi 20\) | 10.3 | \(\phi 6//0.2\) |
| (4 ramos) |
| \(4\phi 12\) | \(2\phi16\) | \(2 \phi 20\) | 4 ramos \(\phi 6//0.2\) |
|---|---|---|---|
| 4.52 | 4.02 | 6.28 | 5.64 |
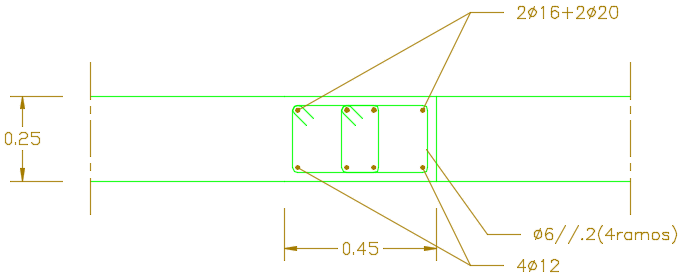
Figure 3: Viga 3
Determinação do Momento Resistente da Viga #3 O momento resistente é determinado através da seguinte equação:
\[\begin{equation} M_{rd}=A_{s} \times f_{yd} \times Z \end{equation}\]em que:
- \(M_{rd}\) é o valor de cálculo do momento flector resistente
- \(A_{s}\) é a área de aço à tração da secção
- \(f_{yd}\) é valor de cálculo da tensão de cedência do aço
- Z é o braço do binário de forças interiores em flexão
De uma forma simplificada, podemos considerar que \(Z=0,81 \times h\), em que “h” é a altura da secção da viga. Somente a área de armadura à tração, ou seja, a armadura inferior, é considerada no cálculo do Momento Resistente. São desprezadas as contribuições do aço à compressão e do betão, à tração.
| \(A_{s} (cm^{2})\) | \(f_{yd} (mPa)\) | h (m) | Z (m) | \(M_{rd} (kN.m)\) |
|---|---|---|---|---|
| 4.52 | 434.78 | 0.25 | 0.2025 | 39.80 |
O valor do Momento Resistente para a viga 3 é de 39.80 kN.m.
Determinação do Esforço Transverso da Viga 3
O cálculo do Esforço Transverso máximo permitido para o Estado Limite Último da viga #1, tendo em conta as condições estruturais implementadas, é feito de acordo com a seguinte equação :
\[\begin{equation} V_{rd}=(\frac{A_{sw}}{S}) \times Z \times f_{yd} \times cot\phi \end{equation}\]em que:
- \(V_{rd}\) é o valor de cálculo do esforço transverso
- \(A_{sw}\) é a área de armadura da secção
- \(S\) é o espaçamento entre armadura
- \(f_{yd}\) é valor de cálculo da tensão de cedência do aço
- Z é o braço do binário de forças interiores em flexão
Tal como na análise da resistência à flexão, também aqui, o valor de Z pode ser calculado por \(Z=0,81 \times h\), em que “h” é a altura da secção da viga.
| \(A_{sw} (cm^{2})\) | S (m) | h (m) | Z (m) | \(f_{yd} (mPa)\) | \(\phi\) | \(V_{rd} (kN)\) |
|---|---|---|---|---|---|---|
| 5.64 | 0.2 | 0.25 | 0.2025 | 434.78 | 1 | 248.28 |
Tendo sido analisadas as presentes condições estruturais, e respeitando os níveis de segurança recomendados pelo EC2, o máximo valor de esforço transverso na viga #3, \(V_{rd}\), é de 248.28 kN.
Reforço
\(M_{Rd}\) e \(V_{Rd}\) de Cálculo
| Viga | \(M_{Rd,b} (kN.m)\) | Increase (%) | \(M_{Rd} (kN.m)\) |
|---|---|---|---|
| 1 | 338.79 | 1.3 | 440.43 |
| 2 | 75.19 | 1.3 | 97.75 |
| 3 | 39.80 | 1.3 | 51.74 |
em que,
- \(M_{Rd,b}\) é o atual momento resistente
- \(M_{Rd}\) é o momento resistente pretendido
| Viga | \(V_{Rd,b} (kN.m)\) | Increase (%) | \(V_{Rd} (kN.m)\) |
|---|---|---|---|
| 1 | 248.28 | 1.3 | 322.76 |
| 2 | 248.28 | 1.3 | 322.76 |
| 3 | 248.28 | 1.3 | 322.76 |
em que,
- \(M_{Vd,b}\) é o atual resistência ao corte
- \(M_{Vd}\) é a resistência ao corte pretendida
Reforço à Flexão com chapas metálicas (coladas e em U)
O texto que se segue é elaborado tendo como base a informação das aulas de CRE.
- As chapas de aço a usar não devem ter uma resistência muito elevada, de modo a não ser necessário uma grande deformação para mobilizar a sua capacidade resistente. Sendo portanto utilizado um aço S235.
- Deve ser garantida a preparação da superfície de betão e das chapas de metal, antes da sua instalação. Quaisquer impurezas devem ser removidas antes da instalação. Se necessário, remover secções de betão degradado.
- Para a Viga #2 e #3, a ligação é feita através de resina que deve ter uma espessura entre 1 e 3 mm. A espessura das chapas metálicas deve ser entre 3 e 5 mm e com a largura inferior a 30cm.
- A espessura da resina ou o contributo desta à resistência da viga ao momento flector, é desprezado nos cálculos de reforço.
As expressões usadas no cálculo do reforço a flexão com chapas, são apresentadas a seguir:
Cálculo da Altura Útil da Secção Transversal, d
Com a introdução da chapa metálica na parte inferior da viga, é necessário agora calcular o \(d_{eq}\) para a peça. O tipo de aço a usar no reforço é S235 em que o \(\gamma_{q}=1,5\):
\[f_{syd,chapa}= \frac {235}{1,5}=156,7 mPa\]
A relação entre o tipo de aço existente e o novo tipo de aço da chapa, é estabelecido através da relação
\[A_{s,rh}= A_{chapa} \times \frac{f_{syd,chapa}}{f_{syd}}\]
em que o \(f_{syd}\) da armadura existente, é de 434.78 mPa.
A determinação da altura útil equivalente da secção, é feita de acordo com a seguinte expressão:
\[\begin{equation} d_{eq}=\frac {A_{s}\times d +A_{s,rh} \times d_{r} }{A_{s} + A_{s,rh} } \end{equation}\]Os valores da altura útil para cada umas das vigas é
- Viga #1, a altura útil da armadura é d=
45.0cm, e para \(d_{r}=\)50.15cms. - Viga #2, a altura útil da armadura é d=
22.5cm, e para \(d_{r}=\)25.25cms. - Viga #3, a altura útil da armadura é d=
22.5cm, e para \(d_{r}=\)25.25cms.
| Viga | \(b_{r},cm\) | \(A_{s},cm^{2}\) | \(t_{s},cm\) | \(A_{chapa},cm^{2}\) | \(A_{s,rh}, cm^{2}\) | d, cm | \(d_{r},cm\) | \(d_{eq},cm\) |
|---|---|---|---|---|---|---|---|---|
| 1 | 30 | 19.24 | 0.3 | 9. | 3.25 | 45 | 50.15 | 45.74 |
| 2 | 30 | 8.54 | 0.3 | 9. | 3.25 | 22.5 | 25.25 | 23.26 |
| 3 | 30 | 4.52 | 0.3 | 9. | 3.25 | 22.5 | 25.25 | 23.65 |
Percentagem Mecânica de Armadura
\[\begin{equation} \omega =\frac { { A }_{ s } }{ bd } \times \frac { { f }_{ syd } }{ { f }_{ cd } } \end{equation}\]Valor Reduzido do Momento Fletor
\[\begin{equation} \mu =\frac {M_{rd}} {b \times d^{2} \times f_{cd}} \end{equation}\] \[\begin{equation} \mu =\omega (1-0.5\omega ) \end{equation}\]Valor de Cálculo do Momento Fletor Resistente
\[\begin{equation} M_{Rd}=\mu \times b \times d^{2} \times f_{cd} \end{equation}\]| Viga | \(A_{s,armd},cm^{2}\) | \(A_{s,rh}, cm^{2}\) | \(A_{s}, cm^{2}\) | b,m | \(d_{eq},m\) | \(f_{cd}, mPa\) | \(f_{syd},mPa\) | \(\omega\) | \(\mu\) | \(M_{Rd},kN.m\) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 19.24 | 3.25 | 22.49 | 0.30 | 0.4574 | 16.7 | 434.78 | 0.43 | 0.34 | 356.38 |
| 2 | 8.54 | 3.25 | 11.79 | 0.45 | 0.2326 | 16.7 | 434.78 | 0.29 | 0.25 | 101.65 |
| 3 | 4.52 | 3.25 | 7.77 | 0.45 | 0.2365 | 16.7 | 434.78 | 0.19 | 0.17 | 71.46 |
Conclusão: Reforço à Flexão com chapas metálicas coladas
A viga #1, devido à sua geometria e para facilidade de instalação, é calculada como tendo o formato em “U”, com 3 mm de espessura na base e 2mm de espessura nos lados. Podemos tirar partido da geometria da peça e garantir a segurança tanto aos momentos fletores como às forças de corte, como desenvolvido na secção 1.3.3 deste trabalho.
- As chapas foram dimensionadas tendo em conta as seguintes limitações:
- Espessura minima de 3mm
- Espessura máxima de 5mm
- A largura deve ser igual ou inferior a 30 cms
- Essas limitações foram conseguidas para as Vigas #2 e #3. Mantendo a espessura miníma de 3mm e a largura máxima de 30 cms de modo a conseguir a maior aproximação possível entre a largura da placa metálica e da base da viga de betão.
Reforço ao corte com chapas metálicas
Todas as vigas, devido ao aumento do esforço de corte em 30%, têm que ser dimensionadas para uma capacidade de resistência a uma força de corte de 322.76kN, o que significa um aumento de 74.48 kN em relação ao esforço máximo corrente. No entanto, esse valor tem que ser reduzido por um quoeficiente de 0.9.
Força de Corte de Cálculo, \(V_{Rd,ref}\)
Cálculo da Área de Aço necessária \(\frac{A_{sw}}{S}\)
\[\begin{equation} V_{Rd,ref}=(\frac{A_{sw}}{S}) \times Z \times \frac{f_{ywd}}{1,5} \times cot \theta \end{equation}\]O valor da \(cot \theta = 1\)
Descricao Resultados
0 F. de Corte de Calculo (kN) 63.390000
1 Z: Comprimento do braco (m) 0.429300
2 fywd (mPa) 235.000000
3 Asw/S Necessario (m2) 0.000723
Descricao Resultados
0 F. de Corte de Calculo (kN) 63.390000
1 Z: Comprimento do braco (m) 0.202500
2 fywd (mPa) 235.000000
3 Asw/S Necessario (m2) 0.001532Dimensionamento da chapa e espaçamento, \(\frac{A_{sw}}{S}\)
Como calculado anteriormente, a \(\frac{A_{sw}}{S}=7.23 cm^{2}\) para a Viga #1, sendo aplicado uma chapa de cada lado da viga de betão (2 ramos):
\[\frac {2 \times b \times e}{S}=7.23cm^{2}\]
Descricao Resultados
0 Asw/S (cm2) 7.230000
1 Espessura da chapa, e (cm) 0.200000
2 Largura da Chapa, b (cm) 5.000000
3 Distancia entre chapas, S (m) 0.276625Devido à geometria das vigas #2 e #3, não é viável a utilização de chapas metálicas sem que primeiro a geometria seja alterada. O desenvolvimento desta opção de reforço é feito na secção 1.4.
Reforço à flexão com encamisamento em betão armado
Parâmetros de Cálculo
O reforço à flexão em encamisamento 1 em betão armado, será feito só para as vigas #2 e #3.
- Viga #2 - O acréscimo de 30% do esforço flector, provoca um aumento de 22.56 kN.m.
- Viga #3 - O acréscimo de 30% do esforço fletor, provoca um aumento de 11.94 kN.m.
- O recobrimento em betão armado será de 10 cms minímo em x-x e em y-y. Ou seja, as dimensões finais de acréscimo em betão armado para ambas as vigas será de 0,65m de largura, 0,35m de altura e ao longo de toda a viga existente.
- É ignorado a contribuição da armadura existente ao acréscimo de tensão
- O betão a ser usado deve ser de classe superior ao existente, sendo por isso usado um betão C30/37, com \(f_{cd}=20 Mpa\).2
Encamisamento Viga #2
Descricao Resultados
0 Momento Resistente (kN/m) 22.56
1 Altura Total h (m) 0.35
2 d (m) 0.315
3 fcd (mPa) 20
4 b (m) 0.65
5 Momento Reduzido 0.0174894
6 W 0.0176450630428535
7 fsyd (mPa) 434.78
8 Area armadura (cm2) 1.66191023415256Encamisamento Viga #3
Descricao Resultados
0 Momento Resistente (kN/m) 11.94
1 Altura Total h (m) 0.35
2 d (m) 0.315
3 fcd (mPa) 20
4 b (m) 0.65
5 Momento Reduzido 0.00925635
6 W 0.00929959333156116
7 fsyd (mPa) 434.78
8 Area armadura (cm2) 0.875887453257808Momentos Negativos
Verificação da resistência à flexão da armadura superior, após a introdução do reforço estrutural na viga. Também aqui, é considerado um aumento de 30% da capacidade resistente à flexão.
| Viga | \(A_{s},cm^{2}\) | \(f_{yd},mPa\) | h,m | Z,m | \(M_{rd},kN.m\) | + 30% | \(M_{rd,calc}^{-} ,kN.m\) |
|---|---|---|---|---|---|---|---|
| 1 | 8.04 | 434.78 | 0.5 | 0.405 | 141.57 | 1.3 | 184.041 |
| 2 | 16.59 | 434.78 | 0.25 | 0.2025 | 146.06 | 1.3 | 189.878 |
| 3 | 10.3 | 434.78 | 0.25 | 0.2025 | 90.68 | 1.3 | 117.884 |
Viga 1 - Verificação aos Momentos Negativos
Para a viga #1, é necessário fazer o reforço aos momentos negativos que existem nas duas extremidades da viga. Um método possível seria o reforço através da introdução de varões na armadura superior, mas no entanto, este método significa a necessidade da remoção do betão na parte superior de modo a ter acesso à armadura existente. É portanto um método que envolve bastante mão-de-obra e que pode danificar areas de betão associadas à viga, como os pilares, devido à vibração das máquinas utilizadas no corte e remoção do betão.
Também não existe nenhuma informação referente à qualidade do betão na parte superior da viga, o que leva a supor que ele se encontra em bom estado de preservação sem sinais de degradação. A introdução de armadura, iria obrigar à remoção de betão em boas condições.
É assim então aconselhável que em vez de adicionar varões, seja adicionada uma chapa metálica de 3mm de espessura e 30cm de largura, nas duas extremidades da viga. O comprimento das duas chapas será um quarto do comprimento da viga, ou seja 1.75 metros. Fica assim garantido (e em excesso) o reforço às necessidades adicionais à armadura superior, ao mesmo tempo que se garante a facilidade e rapidez da instalação.
Devido à espessura da chapa metálica (3mm), facilmente é disfarçado a localização aonde esta é instalada. Caso seja necessário (e não existe nenhuma razão para crer que o seja), a chapa pode ser embutida na laje, de forma que a sua superficie fique ao mesmo nível que a da laje.
Viga 2 - Verificação aos Momentos negativos
Descricao Resultados
0 Momento Resistente (kN/m) 184.04
1 Altura Total h (m) 0.5
2 d (m) 0.45
3 fcd (mPa) 16.7
4 b (m) 0.45
5 Momento Reduzido 0.120937
6 W 0.129295374272433
7 fsyd (mPa) 434.78
8 Area armadura (cm2) 10.0566868748746
9 Area de Betao, m2 0.225
10 Area Maxima armadura,cm2 90
11 fctm, mPa 2.2
12 fyk, mPa 500
13 Area minima armadura, cm2 2.3166
14 Verificacao Area minima, cm2 2.6325
Verificacao: As,min = 2.3166 cm2 > 0,0013xbtxd = 2.6325000000000003 cm2
Verifica Condicoes pelo ECConclusão para o Momento Máximo Negativo para a Viga 2
Verifica as condições de segurança, não sendo necessário adicionar nenhuma armadura superior de reforço.
Viga 3 - Verificação aos Momentos Negativos
Descricao Resultados
0 Momento Resistente (kN/m) 117.88
1 Altura Total h (m) 0.5
2 d (m) 0.45
3 fcd (mPa) 16.7
4 b (m) 0.45
5 Momento Reduzido 0.0774615
6 W 0.0807193440843982
7 fsyd (mPa) 434.78
8 Area armadura (cm2) 6.27840843317111
9 Area de Betao, m2 0.225
10 Area Maxima armadura,cm2 90
11 fctm, mPa 2.2
12 fyk, mPa 500
13 Area minima armadura, cm2 2.3166
14 Verificacao Area minima, cm2 2.6325
Verificacao: As,min = 2.3166 cm2 > 0,0013xbtxd = 2.6325000000000003 cm2
Verifica Condicoes pelo ECConclusão para o Momento Máximo Negativo para a Viga 3
Verifica as condições de segurança, não sendo necessário adicionar nenhuma armadura superior de reforço.
Conclusão
Resultados das várias análises
Reforço à flexão com chapas metálicas coladas
De acordo com os resultados obtidos na secção 1.3, é apresentado os resultados finais e a melhor forma encontrada para fazer o reforço das vigas.
| Viga | \(t_{s} (cm)\) | \(b_{r} (cm)\) | Aço | Informação |
|---|---|---|---|---|
| 1 | 0.3 | 30.6 | S235 | Necessário a colocação de buchas metálicas |
| 2 | 0.3 | 30 | S235 | |
| 3 | 0.3 | 30 | S235 |
- Em que \(t_{s}\) é a espessura da chapa metálica e \(b_{r}\) a sua largura. As chapas da vigas 2 e 3, são ligadas por colagem de resina epoxy. Para a viga #1, é utilizado um perfil metálico em “U” com 30.6 cms de largura (30 cms de base + [2 x 3mm de abas laterais]).
- Para as vigas #1 e #2, o momento máximo é considerado a meio vão, admitindo uma distribuição da carga equivalente e que ambos os apoios das vigas sejam encastramentos. Para a viga #3, o momento máximo é obtido na ligação com pilar inferior.
Reforço ao Corte com chapas metálicas
De acordo com os resultados obtidos na secção 1.3.3, para a Viga #1, a resistência ao aumento da força de corte é conseguida através da instalação de 2 ramos de chapas, de 5cm de largura, 2mm de espessura, espaçados 25cm. Para a Viga #2 e #3, a solução de chapas metálicas não é a melhor solução a ser realizada, dentro dos atuais parâmetros geométricos da viga.
No entanto, com a alteração da geometria proposta em 1.3.4, torna-se possivel o uso de chapas metálicas para ambas as vigas #2 e #3.
Reforço à Flexão com encamisamento em betão armado
Os resultados obtidos na secção 1.3 deste trabalho, são apresentados na tabela seguinte:
| Viga | Valor de Armadura Calculado: \(A_{s} cm^{2}\) |
|---|---|
| 2 | 1.66 |
| 3 | 0.87 |
A área de armadura miníma recomendada para encamisamento é de \(3 \phi12 = 3,39 cm^{2}\), que é portanto muito superior às exigências de reforço de ambas as vigas.
Momentos negativos Para a viga #1, será necessário introduzir uma chapa metálica em ambos os extremos da viga, na sua parte superior. Para a viga #2 e #3, com o aumento da altura da viga/s provocada pelo encamisamento, cria-se uma situação de reforço indirecto ao momento negativo (armadura superior) pelo aumento do braço (altura Z), não sendo portanto necessário adicional armadura superior.
Solução Final
Viga #1
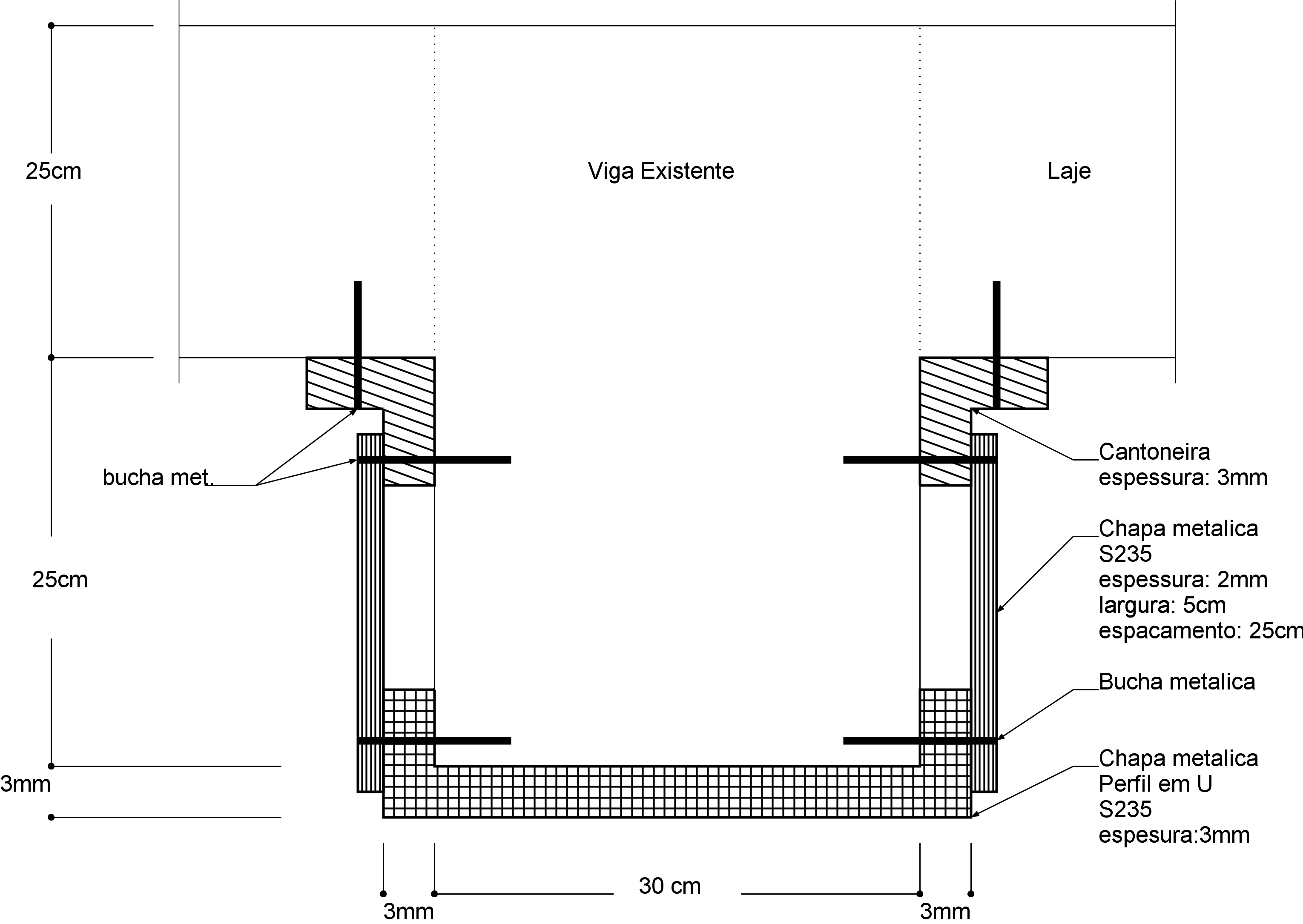
Figure 4: Esquema de reforço proposto para a Viga #1
- Flexão: Colocação de uma chapa metálica S235, de 3mm de espessura e 30.6 cm de largura na parte inferior da viga e fixada com buchas metálicas. Chapa deve ter o mesmo comprimento que a viga e especial atenção deve ser dada à ligação da chapa com os pilares.
- Corte: Colocação de chapas metálicas S235, de 2mm de espessura, 5 cms de largura e espaçadas a 25 cms, de cada lado da viga. As chapas devem ser coladas com resina epoxy e buchas metálicas. No topo, as chapas devem ligar a cantoneira de 3 mm de espessura como exemplificado no desenho que acompanha este documento.
- A Figura em cima, apresenta a solução proposta 3
- Momento Negativo: Chapa metálica S235 de 3mm de espessura e 30 cm de largura e 1,75m de comprimento, aplicada na superfície da laje, por cima da viga, nos dois extremos da viga (ligação viga-pilar). As duas chapas serão coladas resina epoxy (ver secção 1.3.5.1)
Viga #2 e Viga #3
Reforço à flexão: Encamisamento em Betão Armado
Para estas duas vigas, uma solução fácil para aumentar a resistência à flexão e ao corte, será através do encamisamento, criando assim as condições geométricas necessárias.4 .
O encamisamento deverá ter uma espessura miníma de 10cms de forma a a proporcionar a geometria necessária para a aplicação de chapas metálicas, necessárias para resistirem ao acréscimo do esforço transverso.
- Ambas as vigas #2 e #3, terão \(3 \phi 12\) para resistirem à flexão.
- O betão a utilizar é um C30/37
- Cintas/estribos em \(\phi 8//0.30\). Devem ser chumbados na laje existente.
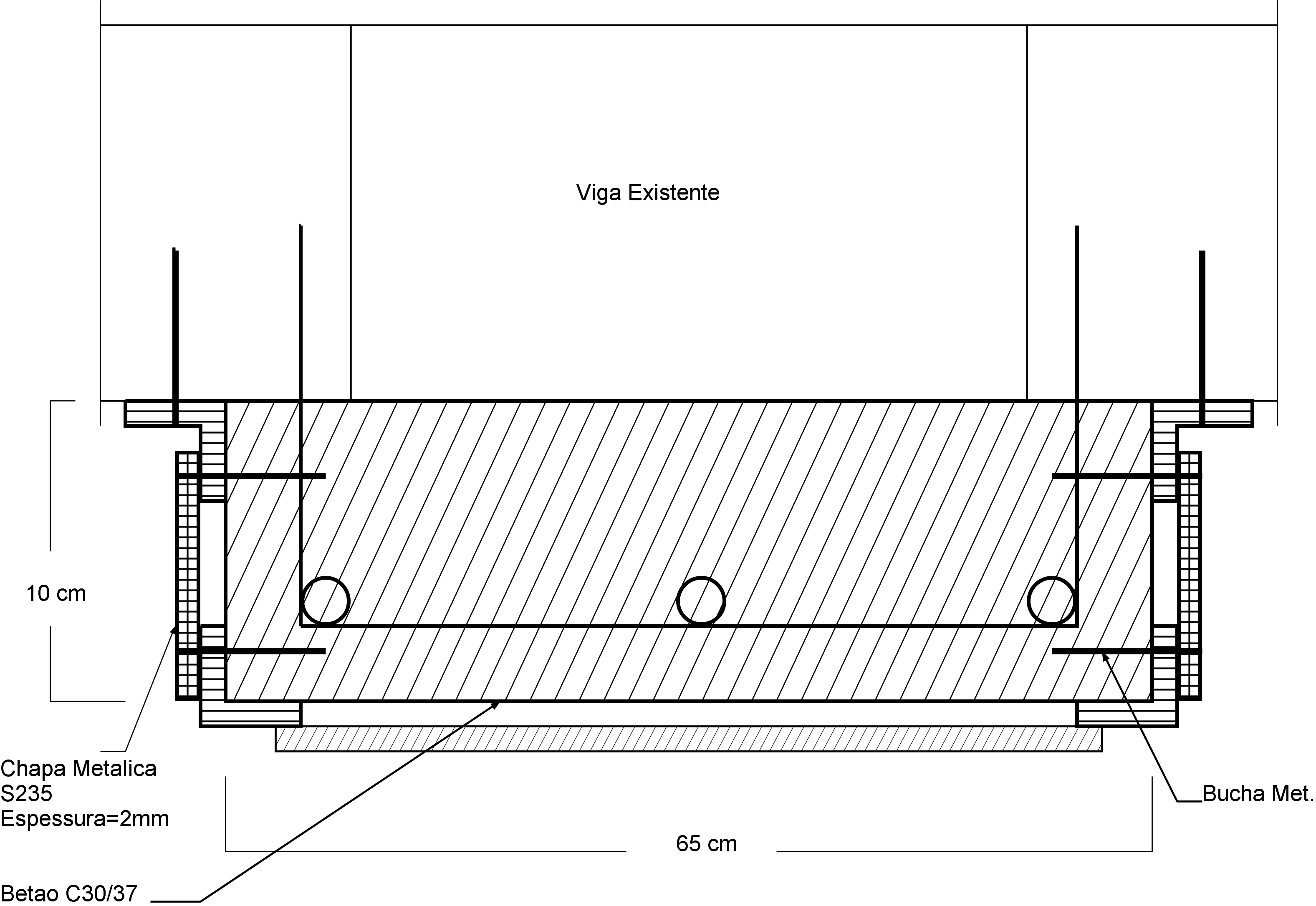
Figure 5: Reforço à flexão e corte para as vigas #2 e #3
Descricao Resultados
0 F. de Corte de Calculo (kN) 74.480000
1 Z: Comprimento do braco (m) 0.283500
2 fywd (mPa) 235.000000
3 Asw/S Necessario (m2) 0.001677
Descricao Resultados
0 Asw/S (cm2) 16.770000
1 Espessura da chapa, e (cm) 0.200000
2 Largura da Chapa, b (cm) 5.000000
3 Distancia entre chapas, S (m) 0.119261Footnotes
1 Na realidade não existe encamisamento propriamente dito, pois a viga encontra-se embutida na laje
2 Embora não tenha sido dada nenhuma informação relativa à classe de betão existente na viga, por questão de segurança, resolveu-se aumentar a classe do tipo de betão para o reforço por encamisamento. As restantes opções de reforço, foram calculadas para um betão de classe C25/30.
3 Figura não se encontra em escala e tem como único objectivo o de auxiliar graficamente o desenvolvimento desta Memória Descritiva. Para o desenho detalhado do reforço, referir às peças desenhadas que acompanham este documento.
4 As soluções apresentadas tentam minimizar o custo e reduzir o impacto na construção existente. Para as Vigas #2 e #3, existirá no entanto uma significativa mudança dimensional, passando agora as vigas a estarem expostas. Tal é assumido que é possível e que não irá interferir com outros elementos do edifício como portas ou janelas
