Análise dos deslocamentos devido a acção sísmica
Segundo o Eurocódigo 8
Luis Moura / 2019-04-07
Exemplo do processo de cálculo através do espectro de resposta, e devido à acção sísmica regulamentar, dos valores de deslocamento de uma estrutura em Leiria. Serviu de base para este processo de cálculo, o trabalho do Professor João Veludo (Veludo 2019), da ESTG em Leiria.
Este post, é criado na sequência de um outro - Espetro de Resposta para prédio localizado em Leiria - Segundo o Eurocódigo 8 - aonde é feito o cálculo dos Espetros de resposta de aceleração e deslocamentos, devidos à acção sísmica regulamentar e determinando os valores da aceleração e deslocamento espectral de um edifício em Leiria, com 1GL.
A versão em PDF deste post, pode ser encontrada aqui.
Estrutura
Estrutura simples1, em betão C30/37, e com 10 metros de altura, localizada no concelho de Leiria. A Classe de Importância é II e encontra-se localizada em um terreno tipo C. Tem um peso próprio de 90 kN e uma sobrecarga de 45 kN com um respectivo \(\psi_{2}=0.6\).
Na tabela Condições iniciais em análise, encontra-se sumariado as condições iniciais, assim como na seguinte figura:

Figure 1: Diagrama da estrutura em análise, na cidade de Leiria
| Nome | Descrição |
|---|---|
| Localização | Leiria |
| Tipo de Terreno | C |
| Classe de Importância | II |
| Betão | C30/37 |
| Carga Própria (CP) | 90 kN |
| Sobrecarga (SC) | 45 kN |
Terreno Tipo C : “Depósitos profundos de areia compacta ou mediamente compacta, de seixo (cascalho) ou de argila rija com uma espessura entre várias dezenas e muitas centenas de metros.”
–Quadro 3.1 - Tipos de Terreno, Eurocódigo 8 (Instituto Português de Qualidade LNEC 2010)
Frequência Própria e Período
Massa
\[ m=\frac{G+\psi_{2} Q}{g}=\frac{90+0,6 \cdot 45}{9,8}=11,94 t n \]
Rigidez
\[ k_{X}=K_{Y}=\frac{3 E I}{L^{3}}=\frac{3 \cdot 33 E 6 \cdot\left[\pi \cdot\left(1,2^{4}-0,8^{4}\right) / 64\right]}{10^{3}}=8086,5 \mathrm{kN} / \mathrm{m} \]
Frequência
\[ f_{X}=f_{Y}=\frac{1}{2 \pi} \cdot \sqrt{\frac{8086,5}{11,94}}=4,14 H z \]
Período
\[ T=\frac{1}{f} \rightarrow T=\frac{1}{4,14}=0,242~ s \]
| Parâmetro | Valor |
|---|---|
| Massa | \(11.94~Ton\) |
| Rigidez | \(8086.4~\frac{kN}{m}\) |
| Frequência | \(4.14~Hz\) |
| Período | \(0.241~s\) |
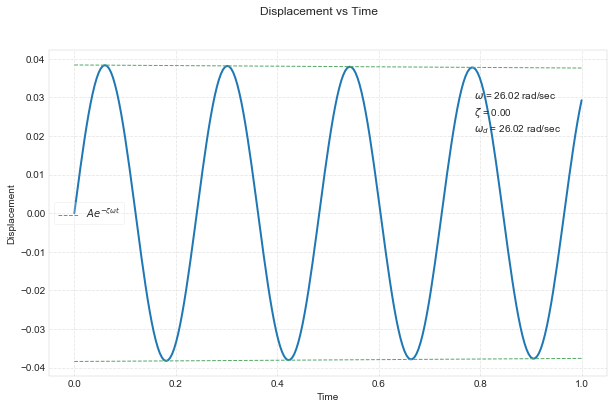
Figure 2: Gráfico para deslocamento no tempo, para o primeiro segundo, e com amortecimento nulo.
Parâmetros pelo Eurocódigo 8
| Parâmetros | Tipo 1 | Tipo 2 |
|---|---|---|
| Localização | Leiria | Leiria |
| Tipo de Terreno | C | C |
| Coeficiente de Importância | 1 | 1 |
| Coeficiente de correcção do amortecimento \(\eta\) | 1 | 1 |
| Aceleração à superfície,\(a_{g}\) | 0.6 | 1.1 |
| Parâmetro \(S_{max}\) | 1.6 | 1.6 |
| Parâmetro \(T_{B}(s)\) | 0.1 | 0.1 |
| Parâmetro \(T_{C}(s)\) | 0.25 | 0.25 |
| Parâmetro \(T_{D}(s)\) | 2 | 2 |
| Parâmetro \(S\) | 1.68 | 1.58 |
Espectro de cálculo para a análise elástica, \(S_{d}(T)\)
O valor de espetro de cálculo2 é feito de acordo com a secção 3.2.2.2 do Eurocódigo 8 (Instituto Português de Qualidade LNEC 2010).
Espectro de cálculo para a análise elástica: “A capacidade dos sistemas estruturais de resistir às acções sísmicas no domínio não linear permite, em geral, efectuar o seu cálculo para resistirem a forças sísmicas inferiores às que corresponderiam a uma resposta elástica linear.”
– Secção 3.2.2.5.(a), Eurocódigo 8 (Instituto Português de Qualidade LNEC 2010)
“O coeficiente de comportamento, q, é uma aproximação da razão entre as forças sísmicas a que a estrutura ficaria sujeita se a sua resposta fosse completamente elástica, com 5 % de amortecimento viscoso, e as forças sísmicas que poderão ser adoptadas no projecto, com um modelo de análise elástica convencional, que continuem a assegurar uma resposta satisfatória da estrutura.”
– Secção 3.2.2.5.(b), Eurocódigo 8 (Instituto Português de Qualidade LNEC 2010)3
Para Acção Sísmica Tipo 1: \[ T_{B} \leq T \leq T_{C} : S_{d}(T)=a_{g} \cdot S \cdot \frac{2,5}{q}=0,6 \times 1,6 \times \frac{2,5}{1}=2,4 \mathrm{m} / \mathrm{s}^{2} \]
Para Acção Sísmica Tipo 2: \[ T_{B} \leq T \leq T_{C} : S_{d}(T)=a_{g} \cdot S \cdot \frac{2,5}{q}=1,1 \times 1,6 \times \frac{2,5}{1}=4,4 m / s^{2} \]
| Intervalo | Sismo Tipo 1 | Sismo Tipo 2 |
|---|---|---|
| \(T_{B}\leq T\leq T_{C}\) | \(2.40~\mathrm{m}/\mathrm{s}^{2}\) | \(4.40~\mathrm{m}/\mathrm{s}^{2}\) |
Esforços e Deslocamentos
Sismo Tipo 1
Determinação4 da força ao nível do grau de liberdade (massa) e do momento flector na base:
\[ F=m . S_{d}(T)=11,94 \times 2.4 =28.65~ \mathrm{kN} \]
\[ M=F . L=28.65 \times 10=286,5~ \mathrm{kNm} \]
Determinação do deslocamento horizontal: \(d_x\)
\[ d_{X}=\frac{F}{K_{X}}=\frac{28,65}{8086,50}=3,54 \times 10^{-3} \mathrm{m}=3,54 \mathrm{mm} \]
Determinação do deslocamento horizontal: \(d_y\)
\[ d_{Y}=\frac{F}{K_{Y}}=\frac{28,65}{8086,50}=3,54 \mathrm{mm} \]
Combinação:
Para análise tridimensional, um determinado efeito X (esforço, deslocamento ou tensão) obtém-se pela combinação das duas direcções em estudo:
\[ X=\pm E_{x} \pm 0,3 E_{y} \]
- \(d_{X}=3,54 \mathrm{mm}\)
- \(d_{Y}=0,3 \times 3,54=1,062 m m\)
\[ d_{max}=\sqrt{3,54^{2}+1,06^{2}}=3,7 \mathrm{mm} \]
Sismo Tipo 2
Determinação5 da força ao nível do grau de liberdade (massa) e do momento flector na base:
\[ F=m . S_{d}(T)=11,94 \times 4.4 =52,54~ \mathrm{kN} \]
\[ M=F . L=52,54 \times 10=525,4~ \mathrm{kNm} \]
Determinação do deslocamento horizontal: \(d_x\)
\[ d_{X}=\frac{F}{K_{X}}=\frac{52,54}{8086,50}=6,50 \times 10^{-3} \mathrm{m}=6,50~ \mathrm{mm} \]
Determinação do deslocamento horizontal: \(d_y\)
\[ d_{Y}=\frac{F}{K_{Y}}=\frac{52,54}{8086,50}=6,50~ \mathrm{mm} \]
Combinação:
Para análise tridimensional, um determinado efeito X (esforço, deslocamento ou tensão) obtém-se pela combinação das duas direcções em estudo:
\[ X=\pm E_{x} \pm 0,3 E_{y} \]
- \(d_{X}=6,50 \mathrm{mm}\)
- \(d_{Y}=0,3 \times 6,50=1,95 ~ mm\)
\[ d_{max}=\sqrt{6,5^{2}+1,95^{2}}=6,78 ~ \mathrm{mm} \]
Resultados
| Parâmetro | Sismo Tipo 1 | Sismo Tipo 2 |
|---|---|---|
| \(S_{d}(T)~\)intervalo\(~T_{B}\leq T\leq T_{C}\) | \(2.40~\mathrm{m}/\mathrm{s}^{2}\) | \(4.40~\mathrm{m}/\mathrm{s}^{2}\) |
| Força, \(F\) | \(28.65~kN\) | \(52.54~kN\) |
| Momento, \(M\) | \(286.5~kNm\) | \(525.4~kNm\) |
| Deslocamento no eixo \(x\), \(d_{x}\) | \(3.543~mm\) | \(6.50~mm\) |
| Deslocamento no eixo \(y\), \(d_{y}\) | \(3.543~mm\) | \(6.50~mm\) |
| Combinação \(X=\pm E_{x} \pm 0,3 E_{y}\) | \(3.70~mm\) | \(6.78~mm\) |
Referências
Instituto Português de Qualidade LNEC. 2010. “Eurocódigo 8 – Projecto de Estruturas Para Resistência Aos Sismos Parte 1: Regras Gerais, Acções Sísmicas E Regras Para Edifícios.”
Veludo, João. 2019. “Resposta a Ações Sísmicas. Espectro de Resposta.” Edited by Escola Superior de Tecnologia e Gestão.
A análise dos parâmetros do espetro de resposta para uma estrutura em Leiria, foi previamente feita no trabalho “Espetro de Resposta para prédio localizado em Leiria”.↩
\(a_{\mathrm{g}},~ S,~T_{\mathrm{B}}, ~ T_{\mathrm{C}}, ~\mathrm{e}~ T_{\mathrm{D}}\) são calculados de acordo com a secção 3.2 do Eurocódigo 8.↩
Por se tratar de uma estrutura isostática, o coef. de comportamento é q=1.↩
Não foram considerados os Efeitos acidentais de torção: “Para ter em conta a incerteza na localização das massas e na variação espacial do movimento sísmico, o centro de massa calculado em cada piso i deve ser deslocado, em cada direcção, em relação à sua posição nominal de uma excentricidade acidental: \(e_{\mathrm{ai}}=\pm 0,05 \cdot L_{\mathrm{i}}\)” –Secção 4.3.2, EC8↩
Não foram considerados os Efeitos acidentais de torção: “Para ter em conta a incerteza na localização das massas e na variação espacial do movimento sísmico, o centro de massa calculado em cada piso i deve ser deslocado, em cada direcção, em relação à sua posição nominal de uma excentricidade acidental: \(e_{\mathrm{ai}}=\pm 0,05 \cdot L_{\mathrm{i}}\)” –Secção 4.3.2, EC8↩
