Espetro de Resposta para prédio localizado em Leiria
Segundo o Eurocódigo 8
Luis Moura / 2019-03-30
Espetros de resposta de aceleração e deslocamentos, devidos à acção sísmica regulamentar, determinando os valores da aceleração e deslocamento espectral de um edifício em Leiria, com 1GL. O texto desta página, encontra-se em formato PDF, e pode ser acedido aqui.
“Se for conhecida a ação e as características dinâmicas do sistema [frequência (\(f\)) e amortecimento (\(\xi\))], é possível determinar a resposta máxima desse sistema durante um determinado intervalo de tempo e que representa uma envolvente da resposta. Se aplicarmos a mesma ação a um sistema com diferentes características dinâmicas (diferente frequência e/ou diferente coeficiente de amortecimento) e determinarmos a resposta máxima obtemos mais um ponto da envolvente da resposta. Se este procedimento for repetido para uma gama de frequências e amortecimentos considerável, o conjunto dos valores máximos de resposta representam o que vulgarmente se designa por espetro de resposta (response spectra). Normalmente determinam-se vários espetros de resposta com um dado amortecimento fazendo o varrimento no domínio da frequência.”
— João Veludo, “Resposta a Ações Sísmicas. Espectro de resposta”, 2019
Identificação do Tipo de Terreno
Identificação do tipo de terreno de acordo com Tabela, do Eurocódigo 8 (Instituto Português de Qualidade LNEC 2010) e a classificação resumida na tabela “Tipo de Terreno”
Descrição do Perfil Estratigráfico: “Depósitos profundos de areia compacta ou mediamente compacta, de seixo (cascalho) ou de argila rija com uma espessura entre várias dezenas e muitas centenas de metros.”
| Tipo de Terreno | \(\upsilon_{s,30} (m/s)\) | \(N_{spt}\) | \(C_{u} (kPa)\) |
|---|---|---|---|
| C | 180-360 | 15-50 | 70-250 |
Classe de Importância e Coeficiente de Importância
Edifício classificado com Classe de Importância II, segundo o Quadro 4.3, do Eurocódigo 8. Para um edifício de Importância II, e de acordo com a mesma secção da norma, o Coeficiente de Importância é 1, \(\gamma_{1}=1,0\).1
| Descrição | Classe de Importância | Coeficiente de Importância |
|---|---|---|
| Prédio/Residencial | II | 1 |
Definição do Zoneamento Sísmico
Para o concelho de Leiria, o Anexo AN.I do EC8 define a zona sísmica e a aceleração para os dois tipos de sismo considerados para Portugal Continental:
| Concelho | Aceleração \(a_{gR} (m/s^{2})\) | Zona Sísmica |
|---|---|---|
| Leiria | 0.6 | 1.5 |
| Concelho | Zona Sísmica | Aceleração \(a_{gR} (m/s^{2})\) |
|---|---|---|
| Leiria | 2.4 | 1.1 |
Aceleração de Cálculo
“Na actual nova regulamentação portuguesa (NA, 2009), são previstos dois tipos de acção sísmica de dimensionamento, sendo um deles (Acção tipo 1) representativo de um sismo de grande magnitude com epicentro na região Atlântica (cenário sísmico designado por “afastado”), e o outro (Acção tipo 2) que representa uma acção com características de um sismo de magnitude moderada com epicentro no território Continental (ou no Arquipélago dos Açores) (cenário “próximo”).”
— Luis Guerreiro (Guerreiro 2010)
O valor de cálculo da aceleração à superfície do terreno e feito de acordo com a secção 3 do Eurocódigo 8.
\[\begin{equation} a_{g}=\gamma_{I} \times a_{gR} \label{eq:Aceleracao-Calculo} \end{equation}\]em que:
- \(a_{g}\) é o valor de cálculo da aceleração à superfície do terreno
- \(\gamma_{I}\) é o coeficiente de importância
- \(a_{gR}\) é a valor de referência da aceleração máxima à superfície do terreno.
No caso do prédio em estudo, o valor de \(\gamma_{I}\) é 1 para ambos os tipos de sismos. Assim, o valor da aceleração de cálculo, \(a_{g}\), é igual à aceleração máxima, \(a_{gR}\), determinada nas tabelas Leiria - Sismo Tipo I e Leiria - Sismo Tipo II.
| Tipo de Sismo | \(a_{g}(m/s^{2})\) |
|---|---|
| I | 0.6 |
| II | 1.1 |
Espetro de Resposta Elástica Horizontal
“O movimento sísmico num dado ponto da superfície do terreno é representado por um espectro de resposta elástica da aceleração à superfície do terreno”
— EC8 (3.2.2.1)
Os cálculos e equações apresentadas, são em acordo com a Secção 3.2.2.2, “Espectro de Resposta elástica horizontal”, do Eurocódigo 8.
\[\begin{equation} \label{Espectro Horizontal} 0\le T\le { T }_{ B }\quad :\quad { S }_{ e }(T)={ a }_{ g }\times S\times \left[ 1+\frac { T }{ { T }_{ B } } \times (\eta \times 2,5-1) \right] \end{equation}\] \[\begin{equation} \label{eq:2} T_{B} \le T \le T_{C} \quad : \quad S_{e}(T)=a_{g} \times S \times \eta \times 2,5 \end{equation}\] \[\begin{equation} \label{eq:Espetro resposta Tc} { T }_{ C }\le T\le { T }_{ D }\quad :\quad { S }_{ e }(T)={ a }_{ g }\times S\times \eta \times 2,5\times \left[ \frac { { T }_{ C } }{ T } \right] \end{equation}\] \[\begin{equation} \label{eq:espectro TD} T_{D} \le T \le 4s \quad : \quad S_{e}(T)=a_{g} \times S \times \eta \times 2,5 \left[ \frac{T_{C}T_{D}}{T^{2}} \right] \end{equation}\]em que:
- \(S_{e}(T)\) é o espectro de resposta elástica
- \(T\) período de vibração de um sistema linear com um grau de liberdade;
- \(a_{g}\) é o valor de cálculo da aceleração à superfície para um terreno do tipo A (\(a_{g}= \gamma_{1} \times a_{gR}\));
- \(T_{B}\) é o limite inferior do período no patamar de aceleração espectral constante;
- \(T_{D}\) é o valor que define no espectro o início do ramo de deslocamento constante;
- \(S\) é o coeficiente de solo;
- \(\eta\) é o coeficiente de correcção do amortecimento, com valor de referência \(\eta = 1\) para 5% de amortecimento viscoso.
No entanto, para Portugal, o Anexo Nacional no artigo NA-3.2.2.2(2)P, diz que para “definição dos espectros de resposta elástica, o valor do parâmetro S deve ser determinado através de”:
- Para \(a_{g} \le 1 m/s^{2}\), \(S\) toma o valor de \(S_{max}\).
- Para \(1m/s^{2} < a_{g} < 4m/s^{2}\), O valor de \(S\) é determinado por \(S=S_{max}-\frac {S_{max}-1}{3} \times (a_{g}-1)\)
- Para \(a_{g} \ge 4m/s^{2}\), o valor de \(S=1,0\)
Os valores da tabela de “Parâmetros dos espectros de resposta elástica” (tabela Parâmetros dos espectros de resposta elástica) foram obtidos do Quadro NA-3.2 e NA-3.3 do Anexo Nacional do Eurocódigo 8.
| Tipo Sismo | \(S_{max}\) | \(T_{B}(s)\) | \(T_{C}(s)\) | \(T_{D}(s)\) |
|---|---|---|---|---|
| I | 1.6 | 0.10 | 0.6 | 2.0 |
| II | 1.6 | 0.10 | 0.25 | 2.0 |
“A definição dos espectros de resposta de dimensionamento é obtida a partir de um espectro de resposta elástico afectado do valor do coeficiente de comportamento. O valor do coeficiente de comportamento depende essencialmente da ductilidade da estrutura. O espectro de resposta elástico é função da sismicidade do local, das características do terreno de fundação e do coeficiente de amortecimento a considerar na estrutura.”
— Luis Guerreiro (Guerreiro 2010)
Cálculo: Parâmetro S para sismo tipo 1
O Cálculo é realizado em Python,2 sendo necessário a introdução dos parâmetros para o tipo de sismo 1.
# Introdução dos parâmetros para tipo 1
Smax_1=1.6
ag_1=0.6
Tb_1=0.1
Tc_1=0.25
Td_1=2
eta_1=1
S_1=N(Smax_1-((Smax_1-1)/3)*(ag_1-1),3)\[S=S_{max}-\frac {S_{max}-1}{3} \times (a_{g}-1)=1,6-\frac {1,6-1}{3} \times (0,6-1)\]
O valor do Parâmetro \(S\)3 para uma situação de um sismo de origem do tipo 1, é de 1.68.
Cálculo: Parâmetro S para sismo tipo 2
O Cálculo é realizado em Python, sendo necessário a introdução dos parâmetros para o tipo de sismo 2.4
# Introdução dos parâmetros para tipo 2
Smax=1.6
ag=1.1
Tb=0.1
Tc=0.25
Td=2
eta=1
S=Smax-((Smax-1)/3)*(ag-1)\[S=S_{max}-\frac {S_{max}-1}{3} \times (a_{g}-1)=1,6-\frac {1,6-1}{3} \times (1,1-1)\]
O valor do Parâmetro \(S\)5 para uma situação de um sismo de origem do tipo 2, é de 1.58.
Espetro de Resposta Elástica Tipo 1
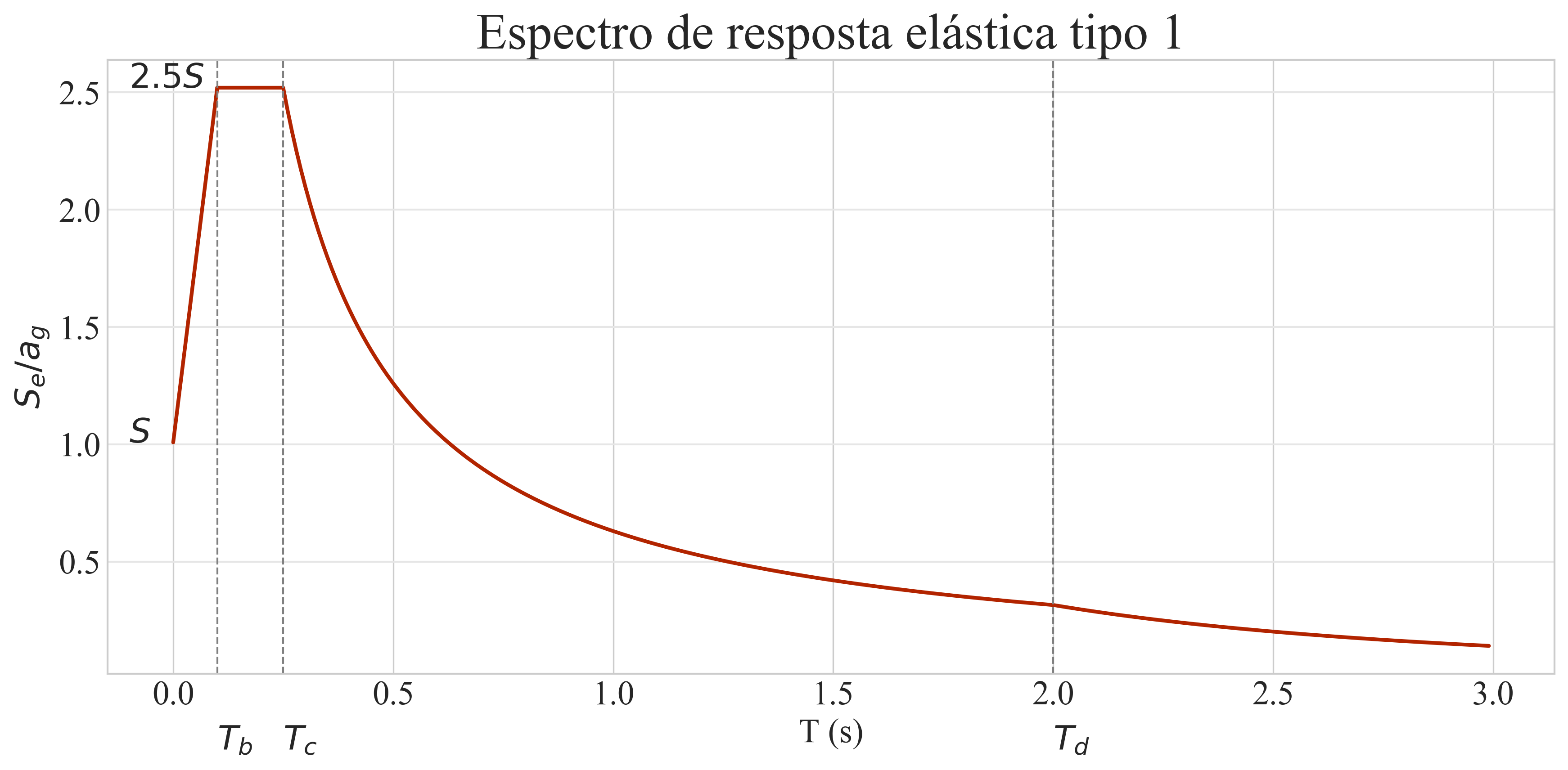
Espectro de Resposta Elástica de tipo 1, para terreno tipo C, no concelho de Leiria e com 5% de amortecimento
“Os valores dos períodos de referência limitam as zonas do espectro de resposta com determinadas características específicas. Assim, a zona do espectro entre o período TB e TC corresponde à zona com valor constante de aceleração espectral. A zona compreendida entre TC e TD por sua vez corresponde à zona de velocidade constante e, por fim, para períodos superiores a TD os deslocamentos espectrais são constantes. Estas características impostas ao espectro de resposta correspondem a um conjunto de propriedades que se verificam, de forma aproximada, na maioria dos espectros de resposta reais.”
— Luis Guerreiro (Guerreiro 2010)
Espetro de Resposta Elástica Tipo 2
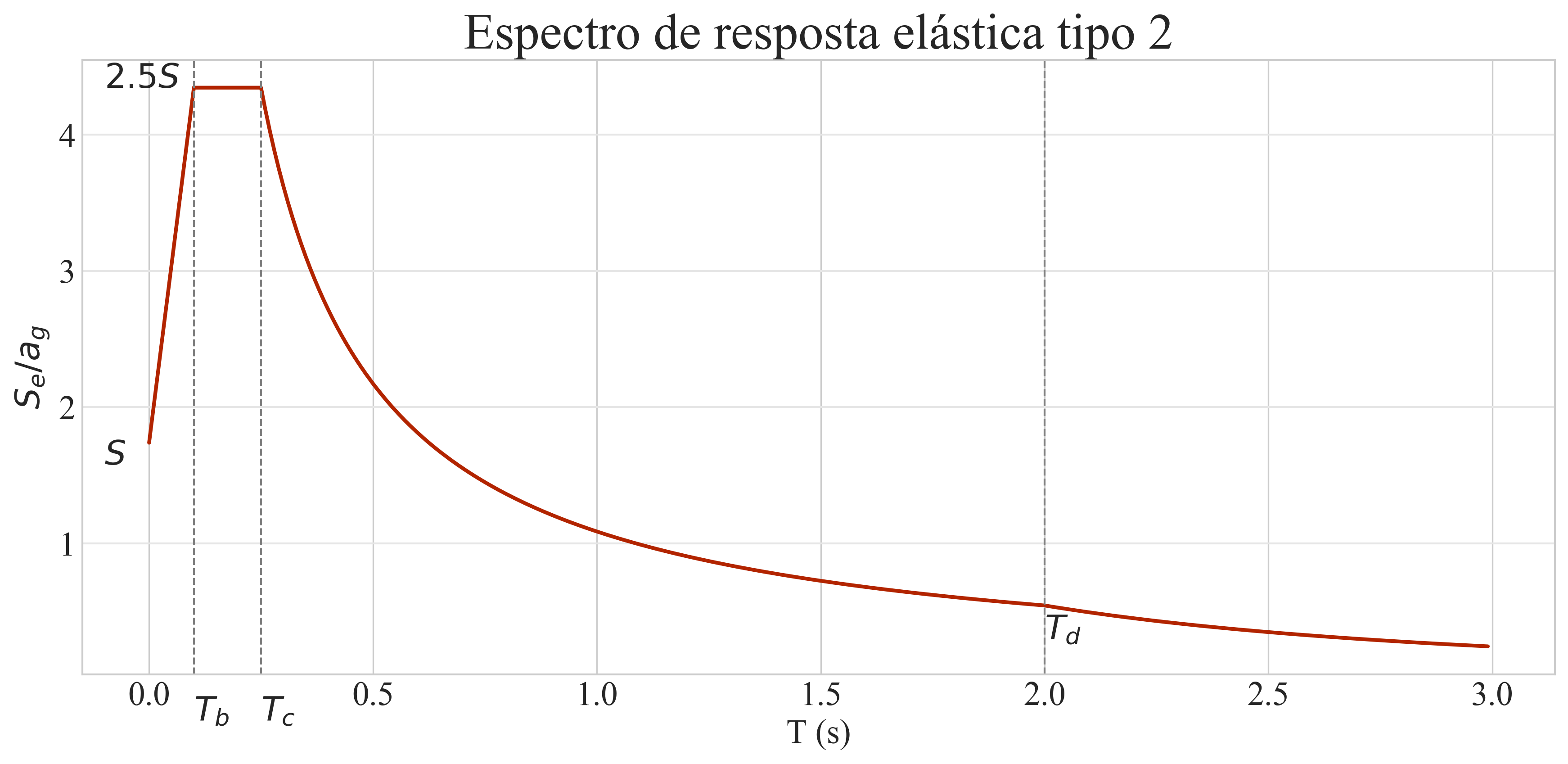
Espetro de Resposta Elástica de tipo 2, para terreno tipo C, no concelho de Leiria e com 5% de amortecimento
Espetro de resposta elástica de acelaração - sumário
A tabela apresenta o sumário dos parâmetros utilizados e seus respectivos valores.
| Parâmetros | Tipo 1 | Tipo 2 |
|---|---|---|
| Localização | Leiria | Leiria |
| Tipo de Terreno | C | C |
| Coeficiente de Importância | 1 | 1 |
| Coeficiente de correcção do amortecimento \(\eta\) | 1 | 1 |
| Aceleração à superfície,\(a_{g}\) | 0.6 | 1.1 |
| Parâmetro \(S_{max}\) | 1.6 | 1.6 |
| Parâmetro \(T_{B}(s)\) | 0.1 | 0.1 |
| Parâmetro \(T_{C}(s)\) | 0.25 | 0.25 |
| Parâmetro \(T_{D}(s)\) | 2 | 2 |
| Parâmetro \(S\) | 1.68 | 1.58 |
| Espetro de Resposta: | — | — |
| \(S_{e}(T=0)\) | 1.008 | 1.738 |
| \(S_{e}(T=T_{B})\) | 2.52 | 4.345 |
| \(S_{e}(T=0.15)\) | 2.52 | 4.345 |
| \(S_{e}(T=0.20)\) | 2.52 | 4.345 |
| \(S_{e}(T=T_{C})\) | 2.52 | 4.345 |
| \(S_{e}(T=0.5)\) | 1.26 | 2.173 |
| \(S_{e}(T=1)\) | 0.63 | 1.086 |
| \(S_{e}(T=1.5)\) | 0.42 | 0.724 |
| \(S_{e}(T=T_{D})\) | 0.315 | 0.543 |
| \(S_{e}(T=2.5)\) | 0.202 | 0.348 |
| \(S_{e}(T=3)\) | 0.14 | 0.241 |
Espetro de Resposta Elástica de Deslocamento
O espetro de resposta elástica de deslocamento, \(S_{\mathrm{De}}(T)\), é obtido directamente da transformação do espetro de resposta elástica de acelaração, \(S_{\mathrm{e}}(T)\) de acordo com o Eurocódigo 8. (Instituto Português de Qualidade LNEC 2010)
\[\begin{equation} S_{\mathrm{De}}(T)=S_{\mathrm{e}}(T)\left[\frac{T}{2 \pi}\right]^{2} \label{eq:desloca} \end{equation}\]Para a figura e figura , o valor de \(T\) é inferior a 4 segundos, sendo este o limite para a qual se pode usar a equação . Para \(T>4s\), o Eurocódigo prevê o uso das equações e
\[\begin{equation} T_{\mathrm{E}} \leq T \leq T_{\mathrm{F}} : S_{\mathrm{De}}(T)=0,025 a_{\mathrm{g}} \cdot S \cdot T_{\mathrm{C}} \cdot T_{\mathrm{D}}\left[2,5 \eta+\left(\frac{T-T_{\mathrm{E}}}{T_{\mathrm{F}}-T_{\mathrm{E}}}\right)(1-2,5 \eta)\right] \label{eq:desloca_1} \end{equation}\] \[\begin{equation} T \geq T_{\mathrm{F}} : S_{\mathrm{De}}(T)=d_{\mathrm{g}} \label{eq:desloca_2} \end{equation}\]| Tipo de Terreno | \(T_{e}(s)\) | \(T_{f}(s)\) |
|---|---|---|
| C | 6 | 10 |
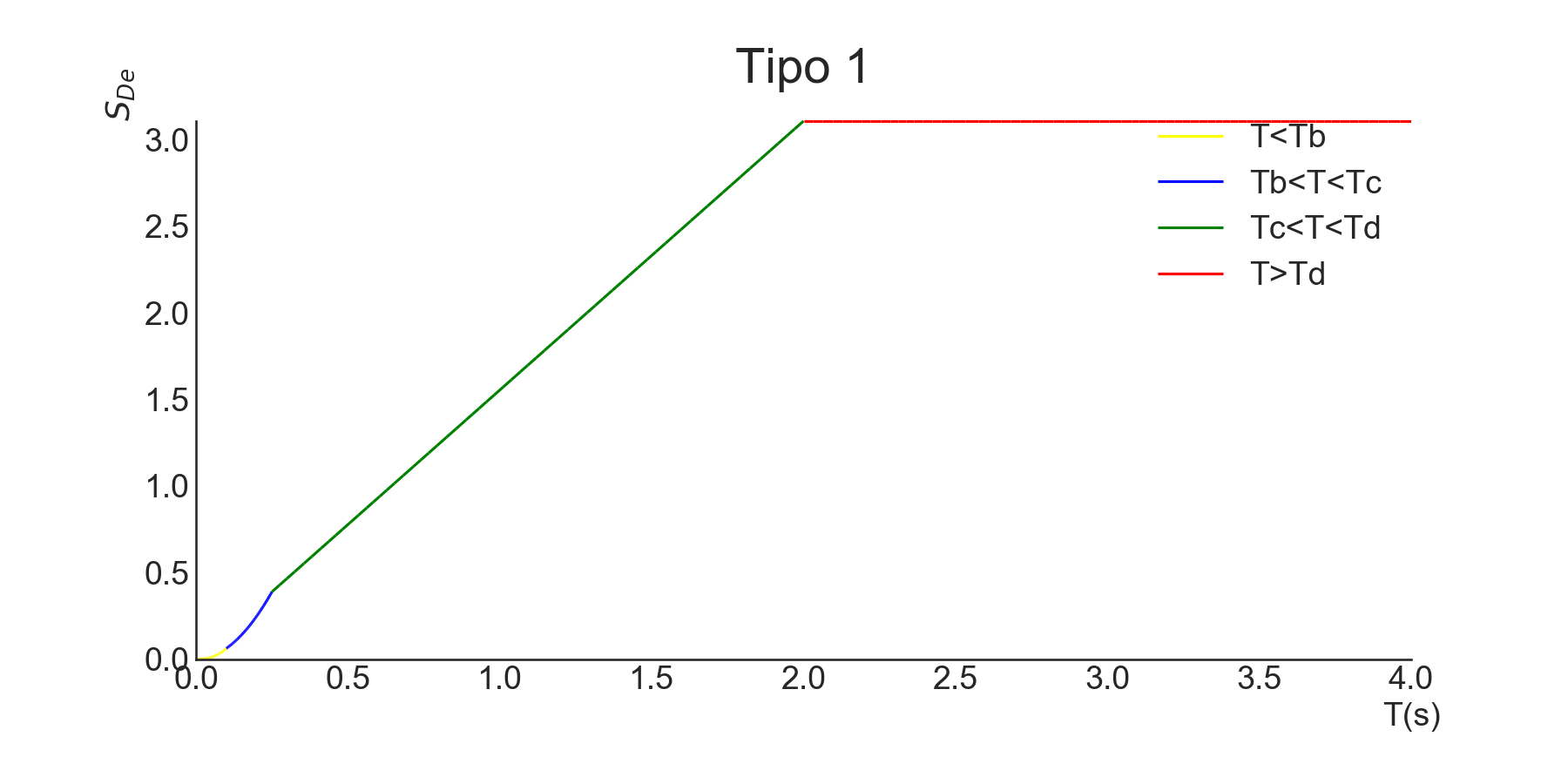
Espetro de resposta elástica de deslocamento para sismo tipo 1, para terreno tipo C, no concelho de Leiria e com 5% de amortecimento
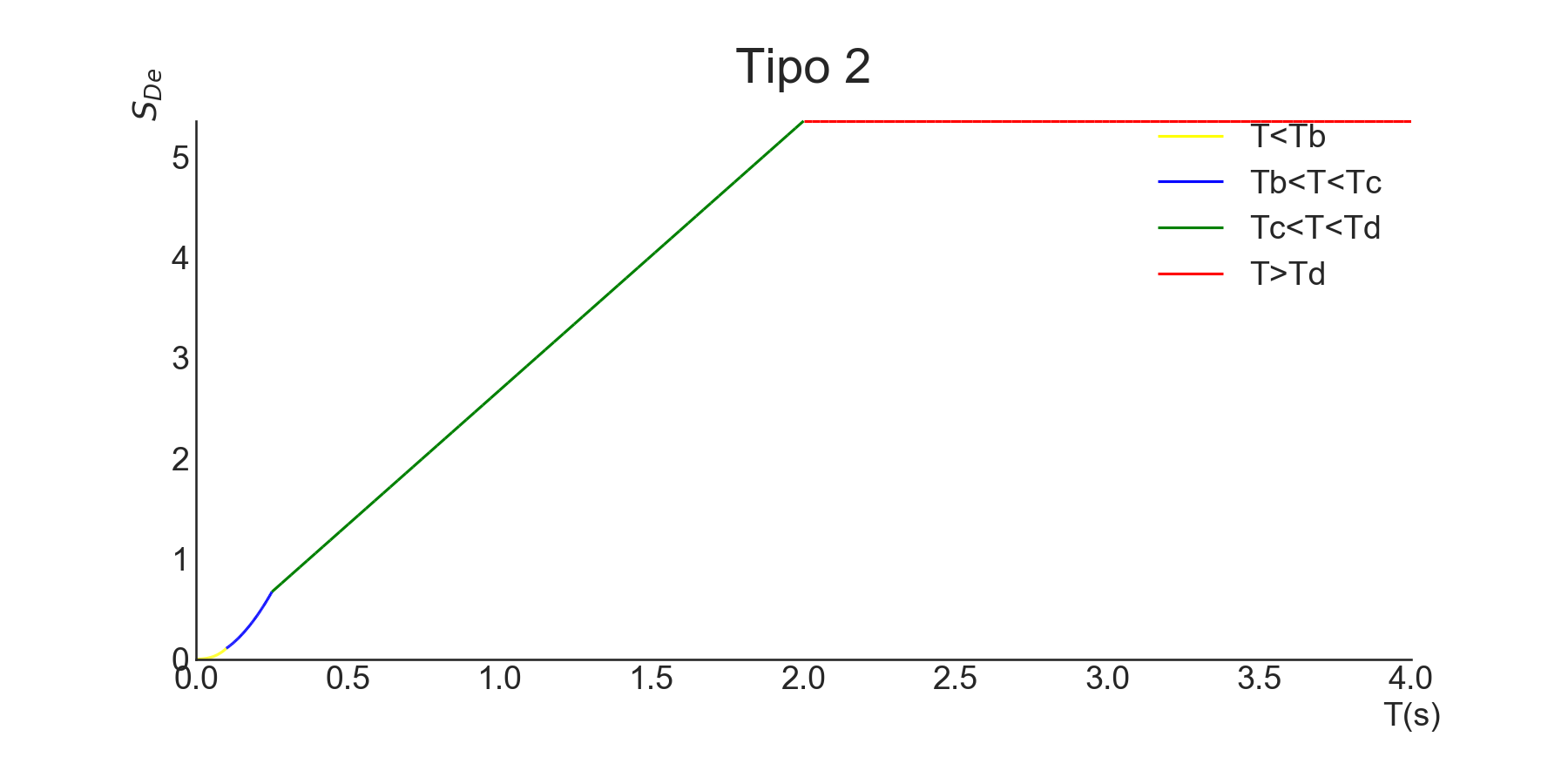
Espetro de resposta elástica de deslocamento para sismo tipo 2, para terreno tipo C, no concelho de Leiria e com 5% de amortecimento
Referências
Guerreiro, Luís. 2010. “Engenharia Sísmica de Pontes.” Edited by Instituto Superior Técnico. http://www.civil.ist.utl.pt/~luisg/textos/Ac%C3%A7%C3%A3o%20S%C3%ADsmica.pdf.
Instituto Português de Qualidade LNEC. 2010. “Eurocódigo 8 – Projecto de Estruturas Para Resistência Aos Sismos Parte 1: Regras Gerais, Acções Sísmicas E Regras Para Edifícios.”
O Quadro NA.II do Anexo Nacional, mantém o valor do coeficiente de importância em 1.↩
Todos os cálculos deste trabalho, foram realizados em Python, usando Jupyter Notebook. Faz parte complementar deste trabalho, um ficheiro em
python(.py), com o todo o código informático utilizado nos cálculos.↩\(S\) é o coeficiente de solo. \(S_{max}\) é obtido da tabela
Parâmetros dos espectros de resposta elástica.↩Todos os cálculos deste trabalho, foram realizados em Python, usando Jupyter Notebook. Faz parte complementar deste trabalho, um ficheiro em
python(.py), com o todo o código informático utilizado nos cálculos.↩\(S\) é o coeficiente de solo. \(S_{max}\) é obtido da tabela
Parâmetros dos espectros de resposta elástica.↩
