TOPSIS - Technique for Order of Preference by Similarity to Ideal Solution
Luis Moura / 2016-04-18
1.0 Lista de Candidatos
Vamos imaginar que existe na nossa empresa uma vaga para a Equipa de Gestão de um Projeto de construção civil. O anúncio da vaga foi colocado em vários websites, e houve uma resposta de 30 pessoas interessadas na oportunidade. Dos 30 candidatos, só 14 foram considerados, tendo sido os outros imediatamente eliminados.
A análise do grupo de candidatos, será feita por um conjunto de cinco critérios, sendo eles:
- Salário Mensal - Quanto é que o candidato espera vir a ganhar mensalmente
- Número de Anos de experiência em Gestão de Obras - Quantos anos o candidato tem a trabalhar em equipas de Gestão de Obras, independentemente de ser equipa de projeto ou de construção.
- Licenciatura em Engenharia Civil
- Distância em kms - A que distância o candidato se encontra do estaleiro-de-obra
Número de Anos de Experiência Gestor de Obras - Quantos anos o candidato tem a gerir projetos de construção civil, podendo estes anos serem como Diretor de Obra ou Encarregado Geral.
Candidato Salario_M Experiencia_anos Licenciatura Distancia_kms GO_anos A 2000 8 não 3 3 B 2500 14 sim 15 0 C 2300 13 sim 25 5 D 1890 7 não 12 1 E 1850 9 não 56 2 F 1950 5 não 22 4 G 2100 18 não 17 8 H 2450 22 sim 11 2 I 1600 2 sim 22 0 J 1750 6 não 62 1 K 1690 4 não 32 0 L 1970 8 não 5 3 M 1500 1 sim 2 0 N 2650 15 não 4 11
1.1 Análise da Base de Dados
Com a informação da tabela, vamos tentar encontrar o melhor candidato para a posição na nossa empresa. Para isso, vamos começar por uma simples análise, recorrendo a gráficos.
1.2 Salário mensal/Licenciatura
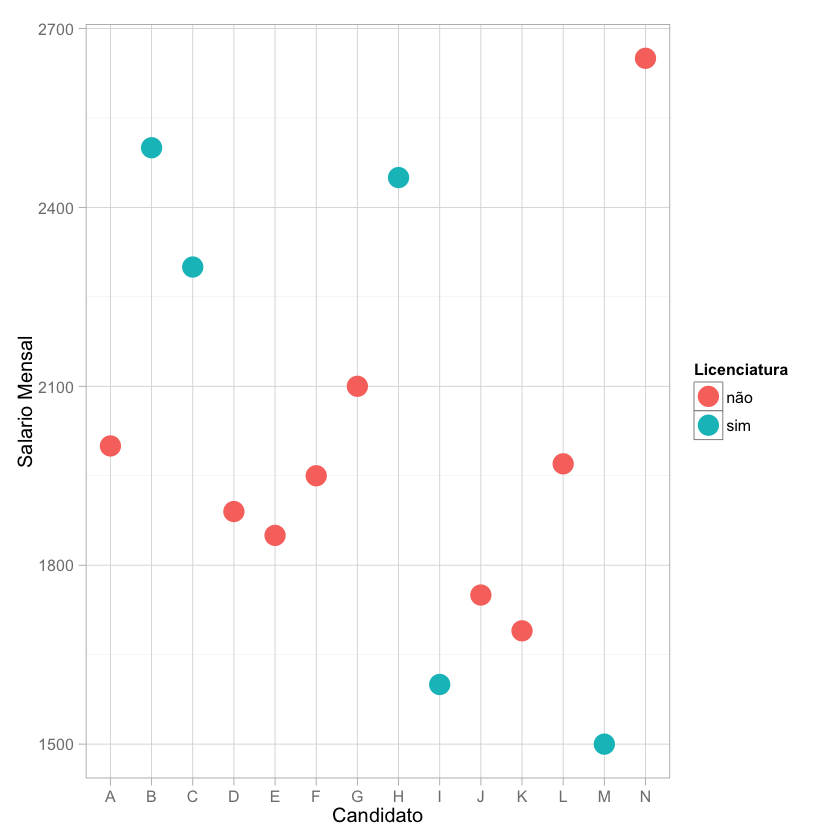
Do gráfico, podemos ver que o Candidato M é o que está disposto a aceitar um salário mensal mais baixo, no entanto, não possuí uma licenciatura em Engenharia Civil. Por outro lado, o Candidato N, é o que espera um salário mensal mais elevado e é licenciado em engenharia civil.
1.3 Número de anos de experiência / Licenciatura em Engenharia Civil
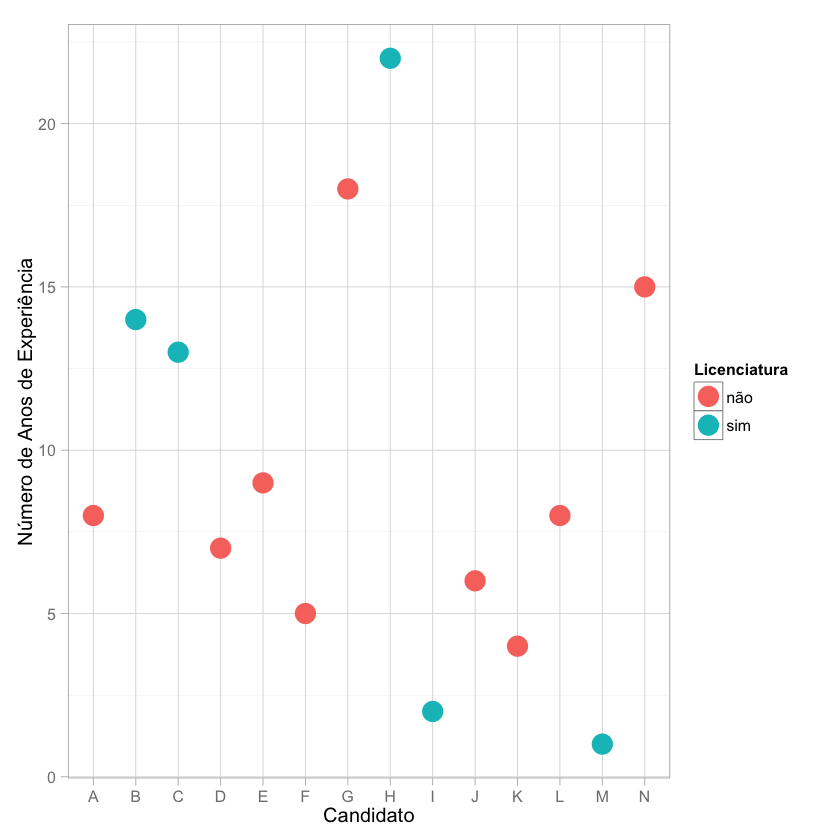
O candidato M, que é o que aceita um salário mais baixo do grupo de candidatos, mas também ;e o que tem menos experiência. Por outro lado, o Candidato H é o que mais anos de experiência tem em equipas de gestão de projetos de construção civil.
1.4 Anos de Experiência como Gestor de Obra / Distância até ao estaleiro-de-obra
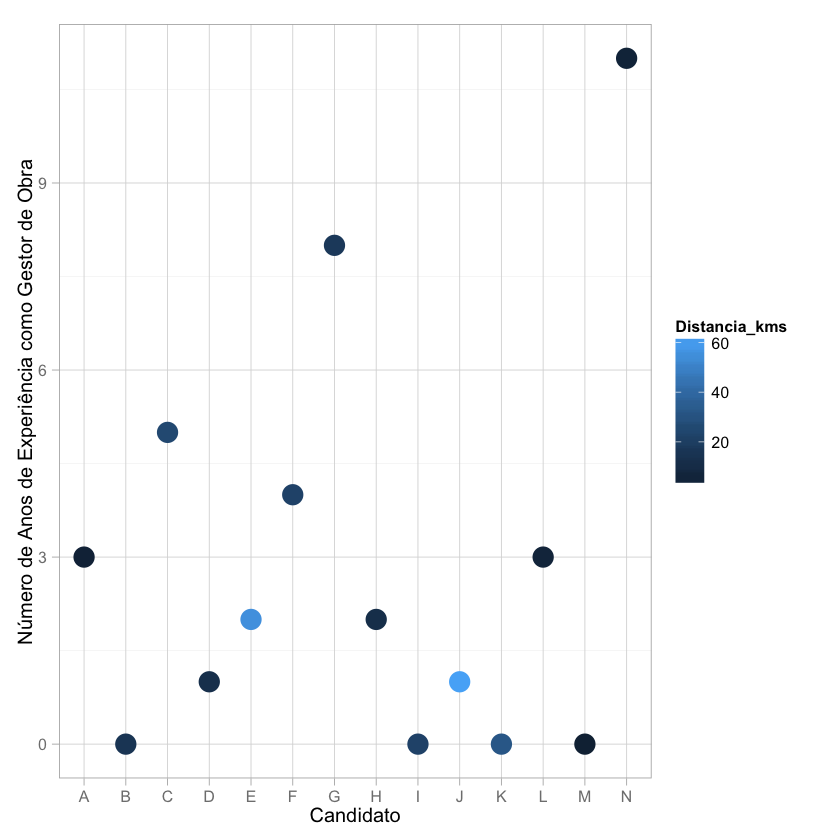
Deste gráfico, podemos tirar as seguintes conclusões: O Candidato N, para além de ser o candidato com mais anos de experiência também mora a uma curta distância do estaleiro de obra, embora seja difícil dizer o posicionamento dele quando comparado com os restantes candidatos (devido à dificuldade na interpretação das cores que representam a distância).
1.5 Juntando a informação obtida
Até ao momento, foram apresentados três gráficos de três possíveis combinações para as variáveis em análise. Embora os gráficos nos possam dar uma ajuda na confirmação de certas possibilidades, torna-se difícil a tomada de decisão baseada somente em eles. No exemplo deste post, a base de dados é pequena, mas em uma situação real, a base de dados pode atingir as centenas de candidatos e os condicionantes, as dezenas.
Um outro problema em análise por gráfico, é a importância que uma variável tem. Como será visto mais à frente, existem variáveis que têm mais importância que outras. Essa importância é difícil de ser passada para o gráfico. Ainda mais difícil, é a criação de um gráfico com todas as variáveis e de acordo com o nível de importância de cada uma.
Para essas situações, em que as variáveis têm um diferente peso na análise, uma técnica possível para análise será através do TOPSIS.
2.0 TOPSIS - Technique for Order of Preference by Similarity to Ideal Solution
Para uma análise com TOPSIS, existem uma série de passos até chegarmos à resposta que pretendemos. O primeiro passo, é a preparação dos dados para análise pelo TOPSIS.
2.1 Preparar os dados da tabela.
No método TOPSIS, não podemos ter texto na tabela, mas somente números. Como a coluna 4, referente à licenciatura, tem duas opções - sim e não - estas opções têm que ser substituídas por números.
O texto da tabela será substituído por “0” quando a resposta é não e “1” quando a resposta é sim à pergunta se o candidato tem uma licenciatura em Engenharia Civil.
| Candidato | Salario_M | Experiencia_anos | Licenciatura | Distancia_kms | GO_anos |
|:---------:|:---------:|:----------------:|:------------:|:-------------:|:-------:|
| A | 2000 | 8 | 0 | 3 | 3 |
| B | 2500 | 14 | 1 | 15 | 0 |
| C | 2300 | 13 | 1 | 25 | 5 |
| D | 1890 | 7 | 0 | 12 | 1 |
| E | 1850 | 9 | 0 | 56 | 2 |
| F | 1950 | 5 | 0 | 22 | 4 |
| G | 2100 | 18 | 0 | 17 | 8 |
| H | 2450 | 22 | 1 | 11 | 2 |
| I | 1600 | 2 | 1 | 22 | 0 |
| J | 1750 | 6 | 0 | 62 | 1 |
| K | 1690 | 4 | 0 | 32 | 0 |
| L | 1970 | 8 | 0 | 5 | 3 |
| M | 1500 | 1 | 1 | 2 | 0 |
| N | 2650 | 15 | 0 | 4 | 11 |
Exemplo: Segue um exemplo para a conversão de texto para valor numérico. O modelo para a conversão depende inteiramente do utilizador, desde que seja consistente e com lógica.
| Condições de acesso ao estaleiro de Obra | é alterado para… |
|---|---|
| Muito boas | 5 |
| Boas | 4 |
| Médias | 3 |
| Más | 2 |
| Muito más | 1 |
Tabela: Exemplo
Passos
No método TOPSIS, existem um série de passos até à obtenção do resultado final. Esses passos são descritos de seguida. Para mais informação sobre o método, é aconselhável ler o trabalho de Hwang, Lai and Liu - ScienceDirect
1º Passo - Normalização
|Candidato | Salario_M | Experiencia_anos | Licenciatura | Distancia_kms | GO_anos |
|:----------:|:---------:|:----------------:|:------------:|:-------------:|:-------:|
| A | 2000 | 8 | 0 | 3 | 3 |
| B | 2500 | 14 | 1 | 15 | 0 |
| C | 2300 | 13 | 1 | 25 | 5 |
| D | 1890 | 7 | 0 | 12 | 1 |
| E | 1850 | 9 | 0 | 56 | 2 |
| F | 1950 | 5 | 0 | 22 | 4 |
| G | 2100 | 18 | 0 | 17 | 8 |
| H | 2450 | 22 | 1 | 11 | 2 |
| I | 1600 | 2 | 1 | 22 | 0 |
| J | 1750 | 6 | 0 | 62 | 1 |
| K | 1690 | 4 | 0 | 32 | 0 |
| L | 1970 | 8 | 0 | 5 | 3 |
| M | 1500 | 1 | 1 | 2 | 0 |
| N | 2650 | 15 | 0 | 4 | 11 |
| Normalizar | 7641 | 42 | 2 | 102 | 16 |
1º Etapa Normalização
É adicionado uma nova linha ao final da tabela, a que eu chamei de “Normalizar”. Em esta linha, serão colocados os resultados da raiz da soma dos valores das colunas ao quadrado: $$ \sqrt{\sum{i=1}^{m} x{ij}^2 } $$
Exemplo do 1º passo para a Normalização da coluna “Salario_M”:
$$ \sqrt{\sum{i=1}^{m} x{ij}^2 } = \sqrt{2000^{2}+2500^{2}+2300^{2}+…2650^{2}}=7641 $$
2º Etapa Normalização
Os resultados desta segunda parte da Normalização, fazem parte da tabela de “2º Passo - Fator de Importância”.
Neste segunda etapa, é necessário dividir cada uma das células da tabela, pelo valor correspondente da linha “Normalizar”.
Exemplo do 2º passo para a Normalização da coluna “Salario_M”:
Todas as células da segunda coluna, serão divididas pelo correspondente valor na linha “Normalizar”que neste caso é 7641. A tabela que se segue, já reflete esta segunda e parte final da Normalização.
$$ r{ij} = \frac {x{ij}} {\sqrt{\sum{i=1}^{m} x{ij}^2 }}; \frac{2000}{7641}=0.262; \frac{2500}{7641}=0.327; …\frac{2650}{7641}=0.347 $$
NOTA: Uma maneira de controlar se até agora não existem erros é com a introdução de uma linha “check” na tabela, em que os resultado, após a aplicação da fórmula que se segue, deve ser sempre 1. Exemplo para a segunda coluna (Salario_M) da tabela:
$$ \sqrt{\sum{i=1}^{m} r{ij}^2 } = \sqrt{0.262^{2}+0.327^{2}+0.301^{2}+…0.347^{2}}=1 $$
2º Passo - Fator de Importância
| Candidato | Salario_M | Experiencia_anos | Licenciatura | Distancia_kms | GO_anos |
|:---------------:|:---------:|:----------------:|:------------:|:-------------:|:-------:|
| A | 0.262 | 0.192 | 0.000 | 0.029 | 0.188 |
| B | 0.327 | 0.336 | 0.447 | 0.147 | 0.000 |
| C | 0.301 | 0.312 | 0.447 | 0.245 | 0.314 |
| D | 0.247 | 0.168 | 0.000 | 0.118 | 0.063 |
| E | 0.242 | 0.216 | 0.000 | 0.548 | 0.125 |
| F | 0.255 | 0.120 | 0.000 | 0.215 | 0.251 |
| G | 0.275 | 0.432 | 0.000 | 0.166 | 0.502 |
| H | 0.321 | 0.528 | 0.447 | 0.108 | 0.125 |
| I | 0.209 | 0.048 | 0.447 | 0.215 | 0.000 |
| J | 0.229 | 0.144 | 0.000 | 0.607 | 0.063 |
| K | 0.221 | 0.096 | 0.000 | 0.313 | 0.000 |
| L | 0.258 | 0.192 | 0.000 | 0.049 | 0.188 |
| M | 0.196 | 0.024 | 0.447 | 0.020 | 0.000 |
| N | 0.347 | 0.360 | 0.000 | 0.039 | 0.690 |
| check | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Importância (%) | 0.250 | 0.200 | 0.150 | 0.050 | 0.350 |
Importância (%)
Para cada uma das variantes, é atribuído um fator de importância. No caso das variáveis em análise, é considerado que o “GO_anos” é a variável mais importante, sendo por isso atribuído 35%. Por outro lado, a “Distancia_kms” foi considerado como sendo o menos importante, com um fator de importância de 5%.
| Variável | Importância (%) |
|---|---|
| Salario_M | 0.25 |
| Experiencia_anos | 0.20 |
| Licenciatura | 0.15 |
| Distancia_kms | 0.05 |
| GO_anos | 0.35 |
| Total | 1.00 |
3º Passo
Peso Normalizado do fator de importância
Multiplicar cada célula da tabela, pelo correspondente fator de importância.
Exemplo para a Coluna “Salario_M”
Em que $r_{ij}$ são os valores das células da tabela do 2ºPasso.
$$ r_{ij}\times f.importância=0.262 \times 0.25= 0.065; 0.327 \times 0.25=0.082…0.347 \times 0.25 =0.087 $$
Verificação - opcional De modo a verificar se não existe nenhum erro de cálculo, adicionar no final da tabela uma linha - check - aonde o resultado, deve ser igual ao fator de importância atribuído à variável da coluna.
$$ \sqrt{0.065^{2}+0.082^{2}+0.075^{2}+…0.087^{2}}=0.250 $$
| Candidato | Salario_M | Experiencia_anos | Licenciatura | Distancia_kms | GO_anos |
|:---------:|:---------:|:----------------:|:------------:|:-------------:|:-------:|
| A | 0.065 | 0.038 | 0.000 | 0.001 | 0.066 |
| B | 0.082 | 0.067 | 0.067 | 0.007 | 0.000 |
| C | 0.075 | 0.062 | 0.067 | 0.012 | 0.110 |
| D | 0.062 | 0.034 | 0.000 | 0.006 | 0.022 |
| E | 0.061 | 0.043 | 0.000 | 0.027 | 0.044 |
| F | 0.064 | 0.024 | 0.000 | 0.011 | 0.088 |
| G | 0.069 | 0.086 | 0.000 | 0.008 | 0.176 |
| H | 0.080 | 0.106 | 0.067 | 0.005 | 0.044 |
| I | 0.052 | 0.010 | 0.067 | 0.011 | 0.000 |
| J | 0.057 | 0.029 | 0.000 | 0.030 | 0.022 |
| K | 0.055 | 0.019 | 0.000 | 0.016 | 0.000 |
| L | 0.064 | 0.038 | 0.000 | 0.002 | 0.066 |
| M | 0.049 | 0.005 | 0.067 | 0.001 | 0.000 |
| N | 0.087 | 0.072 | 0.000 | 0.002 | 0.242 |
| Check | 0.250 | 0.200 | 0.150 | 0.050 | 0.350 |
4º Passo - Escolha dos melhores e piores valores
Piores valores
Da tabela do 3ºPasso, escolher os piores valores, ou seja, o mínimo de cada coluna, no entanto, para a Coluna “Salario_M”, o pior valor será o mais alto (0.087), visto esta coluna lidar com ordenados. Ou seja, quanto mais alto for o valor das células na Coluna “Salario_M”, mais a empresa terá que gastar em ordenado e portanto será considerado um aspeto negativo.
UPDATE: Na coluna “Distancia_kms” também devia ter sido feito a mesma consideração que para a coluna “Salario_M”, visto que pode-se considerar como negativo o quanto maior for a distância desde a residência do candidato até ao estaleiro-de-obra.
Melhores valores
Tal como para os piores valores, mas desta vez escolher o máximo de cada coluna, representativo da melhor solução do grupo para uma dada variável. Mais uma vez a exceção é a coluna “Salario_M”, em que o melhor valor é o mais baixo (0.049), representativo do salário mais baixo do grupo.
Tabela com os resultados dos melhores e piores valores:
| Atributo | Salario_M | Experiencia_anos | Licenciatura | Distancia_kms | GO_anos |
|:--------:|:---------:|:----------------:|:------------:|:-------------:|:-------:|
| + | 0.049 | 0.106 | 0.067 | 0.030 | 0.242 |
| - | 0.087 | 0.005 | 0.000 | 0.001 | 0.000 |
5º Passo - Normalização do 4ºPasso
Até agora a análise tem sido feito por colunas, ou de acordo com as variáveis em análise. A partir de agora a análise será feita por linhas, ou para cada Candidato.
Valores Negativos por Candidato
Para o cálculo que se segue, é necessários os dados das Tabelas do 3º e 4º Passo.
Exemplo para Candidato A: Para o valor de cada célula das colunas do Candidato A* na Tabela do 3º Passo, é subtraído o valor negativo do 4ºPasso, sendo o resultado elevado ao quadrado. O resultados é depois somado aos valores também obtidos para cada uma das células da linha do Candidato A:
$$ A^{-}_{candidato A}= (0.0065-0.087)^{2}+(0.038-0.005)^{2}+0+…(0.066-0)^{2}=0.006 $$
| Candidato | Negativo |
|:---------:|:--------:|
| A- | 0.006 |
| B- | 0.008 |
| C- | 0.020 |
| D- | 0.002 |
| E- | 0.005 |
| F- | 0.009 |
| G- | 0.038 |
| H- | 0.017 |
| I- | 0.006 |
| J- | 0.003 |
| K- | 0.001 |
| L- | 0.006 |
| M- | 0.006 |
| N- | 0.063 |
Valores Positivos por Candidato
Para o cálculo que se segue, é necessários os dados das Tabelas do 3º e 4º Passo.
Exemplo para Candidato A: Para o valor de cada célula das colunas do Candidato A na Tabela do 3º Passo, é subtraído o valor positivo do 4ºPasso, sendo o resultado elevado ao quadrado. O resultados é depois somado aos valores também obtidos para cada uma das células da linha do Candidato A:
$$ A^{+}_{candidato A}= (0.0065-0.049)^{2}+(0.038-0.106^{2}+(0-0.067)^{2}+…(0.066-0.242)^{2}=0.041 $$
| Candidato | Positivo |
|:---------:|:--------:|
| A+ | 0.041 |
| B+ | 0.061 |
| C+ | 0.020 |
| D+ | 0.059 |
| E+ | 0.048 |
| F+ | 0.035 |
| G+ | 0.010 |
| H+ | 0.041 |
| I+ | 0.068 |
| J+ | 0.059 |
| K+ | 0.071 |
| L+ | 0.041 |
| M+ | 0.069 |
| N+ | 0.008 |
6ºPasso - Último passo antes da tomada de decisão
Para este necessário, são necessários os dados das tabelas do 5º Passo.
Exemplo Candidato A: Proximidade à pior solução possível
$$A= \frac{A^{-}}{A^{+}+A^{-}}=\frac{0.006}{0.041+0.006}=0.126$$
Exemplo Candidato B: Proximidade à pior solução possível $$B= \frac{B^{-}}{B^{+}+B^{-}}=\frac{0.008}{0.061+0.008}=0.121$$
| Candidato | Ta |
|:---------:|:-----:|
| A | 0.126 |
| B | 0.121 |
| C | 0.499 |
| D | 0.032 |
| E | 0.091 |
| F | 0.197 |
| G | 0.790 |
| H | 0.290 |
| I | 0.079 |
| J | 0.045 |
| K | 0.020 |
| L | 0.127 |
| M | 0.079 |
| N | 0.889 |
| Max= | 0.889 |
Conclusão
Com os resultados obtidos da tabela do 6º Passo, procuramos o máximo valor na coluna $T_{a}$. O máximo valor, 0.889, correspondente ao Candidato N, é melhor opção de acordo com as condições definidas ao longo do método.
