Dimensionamento de Pilar de Betão Armado
Cálculo segundo o Eurocódigo 2
Luis Moura / 2016-01-06
Introdução
Dimensionamento de pilares em betão armado, de acordo com o Eurocódigo 2 (Comité Europeu de Normalização 2004).
Cálculo estrutural de um pilar em betão armado, que de forma exemplificava, servirá para demonstrar o processo de cálculo perante as normas do Eurocódigo. Todo o cálculo é feito recorrendo a linguagem informática, sendo utilizado Python (Rossum and Drake 2001) e R (R Core Team 2015). Este trabalho é baseado nas notas do Professor Veludo (J.Veludo 2014).
Condições Iniciais
Dimensionar a armadura longitudinal de um pilar com uma secção rectangular de dimensões 80×60 \(cm^{2}\), sujeita aos esforços indicados na figura.

Secção do Pilar
Dados para a análise:
- Esforço Axial: \(N_{Ed}=3000kN\) (compressão)
- Momento: \(M_{Ed,x}=525 kN.m\)
- Momento: \(M_{Ed,y}=1516 kN.m\)
- Aço: S500NR
- Betão: C30/37
- Dimensões do Pilar: \(0.8m \times 0.6m\)
Introdução dos dados no sistema
Mrdx=525 #Momento fletor resistente em x (kN.m)
Mrdy=1516 #Momento fletor resistente em y (kN.m)
N=3000 #Esforço Axial (kN)
bx=0.8 #Largura (m), em x
hx=0.6 #Altura (m), em x
by=0.6 #Largura (m), em y
hy=0.8 #Altura (m), em y
fcd=20*10**3 #tensão rotura betão à compressão (mPa)
fyd=435*10**3 #tensão de cedência à tração no aço (mPa)Introdução das fórmulas
Neste momento podemos introduzir algumas das fórmulas que vamos usar no dimensionamento:
- Momento Reduzido
- Esforço Axial Reduzido
Momento Reduzido, \(\mu\):
\[\mu=\frac{M_{Ed}}{b \times h^{2} \times f_{cd}}\]
Esforço axial reduzido:
\[n=\frac{N_{ed}}{A_{c}\times f_{cd}}\]
Introdução das fórmulas para o Momento Reduzido e Esforço axial reduzido no sistema.
ux=Mrdx/(bx*hx**2*fcd) #Momento reduzido (kN.m)
uy=Mrdy/(by*hy**2*fcd) #Momento reduzido (kN.m)
v=N/(bx*hx*fcd) #Esforço axial reduzido (kN)Resultados para \(\mu_{x}\), \(\mu_{y}\) e \(v\)
Para o Momento Reduzido em X, o resultado é de 0.0911458, para o Momento Reduzido em y, o resultado é de 0.1973958, e para o Esforço Axial Reduzido, o resultado é 0.3125.
Obter área de armadura das tabelas
Com recurso ao ábaco da flexão desviada (H.Barros and J.Figueiras 2012) , é possível obter o valor da taxa mecânica de armadura, \(\omega\). Na obtenção dos resultados, foram admitidas as seguintes hipóteses:
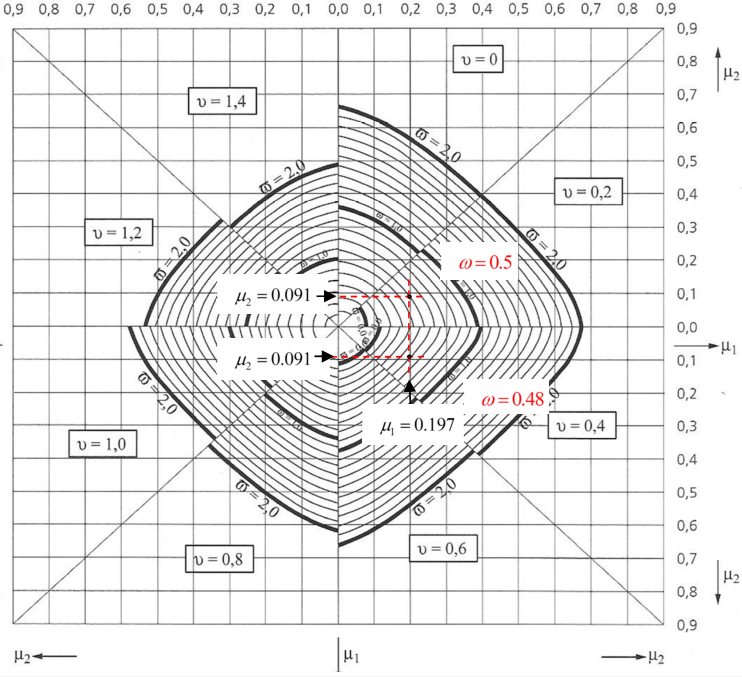
Ábaco para Secções Retangulares com flexão desviada e armadura igualmente distribuida
- Armadura igual nas 4 faces
- \(\mu_{1}\) é o maior valor entre \(\mu_{x}\) e \(\mu_{y}\)
- \(\mu_{2}\) é o menor valor entre \(\mu_{x}\) e \(\mu_{y}\)
- A relação recobrimento/comprimento é igual nas 4 faces e toma o valor de 0.10
Taxa mecânica de Armadura \(\omega\):
\[\omega=\frac{A_{s}\times f_{yd}}{A_{c}\times f_{cd}}\]
Área de Armadura, \(A_{s}\)
\[A_{s}=\omega \times b \times h \times \frac{f_{cd}}{f_{yd}}\]
O valor obtido do ábaco para a taxa mecânica de armadura, \(\omega\) é de 0.489.
w=0.489 #Taxa Mecânica de Armadura
As=w*bx*hx*(fcd/fyd)*10**4 # Area Aço convertida para cm2Área de Armadura
## [1] "Área armadura total/secção = 107.92 cm2."Escolha da armadura: \[4\phi32+16\phi 25 = 110.7cm^{2}\]
Pormenorização
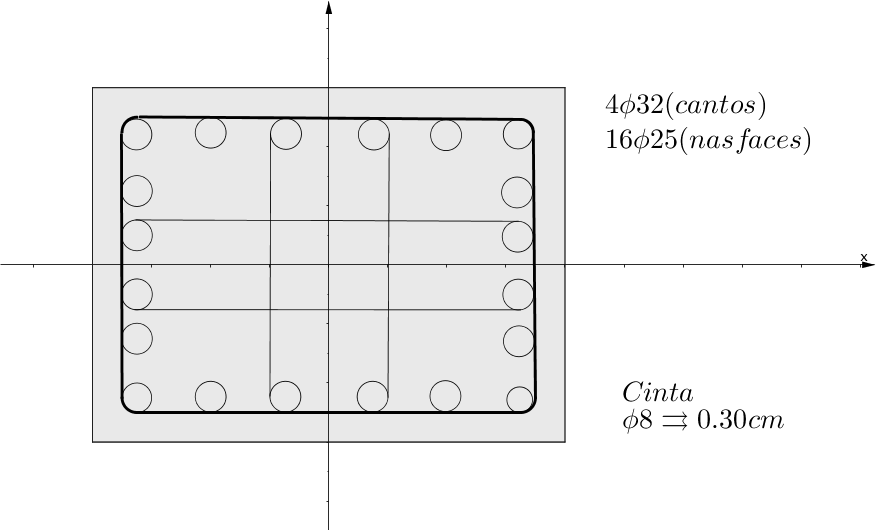
Pormenorização
Bibliografia
Comité Europeu de Normalização. 2004. Eurocódigo 2 - Projeto de Estruturas de Betão. Caparica, Portugal: Instituto Português de Qualidade.
H.Barros, and J.Figueiras. 2012. Tabelas E ábacos de Dimensionamento de Secções de Betão Solicitadas à Flexão E a Esforços Axiais Segundo O Eurocódigo 2. Porto, Portugal: Faculdade de Engenharia da Universidade do Porto.
J.Veludo. 2014. “Apontamentos Teóricos.” Leiria, Portugal: Escola Superior de Tecnologia e Gestão. http://www.ipleiria.pt/estg/.
R Core Team. 2015. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. http://www.R-project.org/.
Rossum, G. Van, and F.L. Drake. 2001. “Python Reference Manual.” Virginia, USA: PythonLabs. http://www.python.org.
